• Quadratic functions
An algebraic expression of the form ax²+ bx + c is called a quadratic function of x.Graph of the quadratic function ax²+ bx + c (a≠ 0)
Procedure:
1. Make a table of corresponding values for x and the function.
2. Plot these points, on a pair of x, f(x) axes.
3. Draw a smooth curve joining the plotted points.
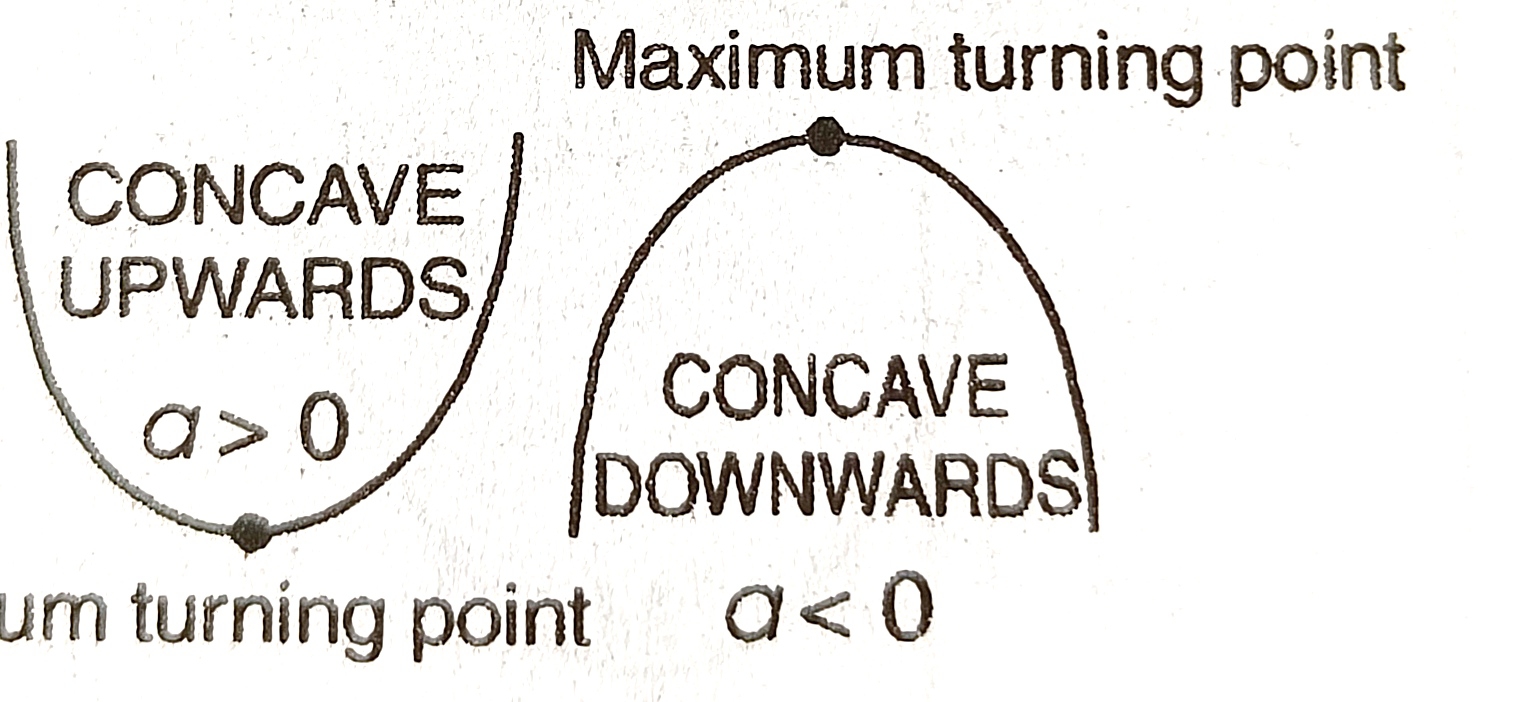
The graph of a quadratic function is parabola. The point at which its direction changes is called its turning point. It is more commonly called the vertex of the parabola.
The graph of the function is concave upwards when a> 0 and concave downwards when a< 0.
NOTE:
Studying the nature and character of the roots of a quadratic by graphing:
The graph give below illustrate the following cases.
Real roots
Case 1: a > 0 Equal roots
Complex roots
Real roots
Case 2: a< 0 Equal roots
Complex roots
a) If the graph cuts the x-axis, the roots of the equation will be real and unequal. Their values will be given by the abscissa of the points of intersection of the graph and the x-axis.
b) If the graph is tangents to the x-axis, the roots are real and equal.
c) If the graph has no points in common with the x-axis, the roots of the equation are imaginary and can not be determined from the graph.
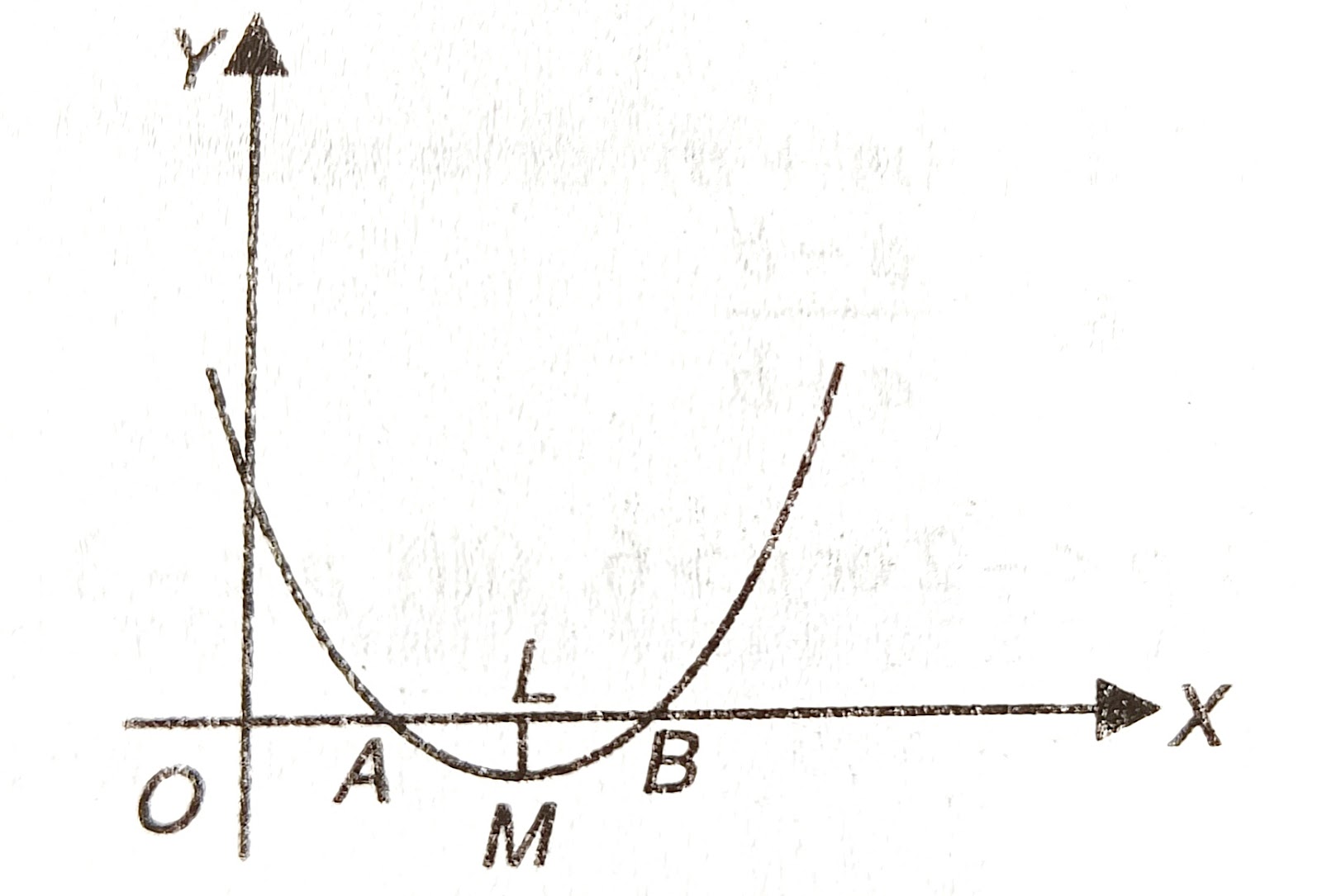
Case 1. When a is positive, i.e., a> 0
Minimum value LM= (4ac - b²)/4a at x = OL = -b/2a
ii) b²- 4ac = 0
Each root = OA
iii) b²- 4ac is -ve
Complex roots. Curve entirely above the x-axis with lowest point M at a height
LM= (4ac - b²)/4a above the x-axis.
Case 2. When a is negative, i.e., a< 0
Real roots OA and OB
Maximum value LM= (4ac - b²)/4a at x= OL = -b/2a
Real and equal roots
Each root= OA
Complex roots. The curve lies entirely below the x-axis and the vertex will be at a distance= (4ac - b²)/4a below OX.
Ex: Graph the expression x²+ x - 6.
Let y= x²+ x -6
Table values:
x y
3 6
2 0
1 -4
0 -6
-1 -6
-2 -4
-3 0
-4 6
Note: Real roots of the equation x²+ x - 6= 0 are x= OP and x= OQ, i.e., x= 2 and x= -3 (on reading from the graph)
Minimum value of the function= LM = -6.25 and occurs when x= -0.5.
Ex: Graph the expression 4- 5x - x².
Let y= 4- 5x - x²
Tables of values:
x y
-6 -2
-5 4
-4 8
-3 10
-2 10
-1 8
0 4
1 -2
Note: Real roots of the equation 4 - 5x - x²=0 are x= OA and x= OB, i.e., x= -5.71, x= 0.71
Maximum value of the function= LM = 10.25, when x= OM when x= OL= -2.5.
The roots of the quadratic equation ax²+ bx + c= 0, a≠ 0 are the x-intercepts of the graph of y= f(x)= ax²+ bx + c.
Ex: The roots x= 0 and x= 3 of the equation 2x(x -3)=0 are the x-intercepts of the graph of y= 2x(x -3) as shown
In this case graph cuts the x-axis at two points because there are two real and distinct roots. In the formula the part b²- 4ac > 0
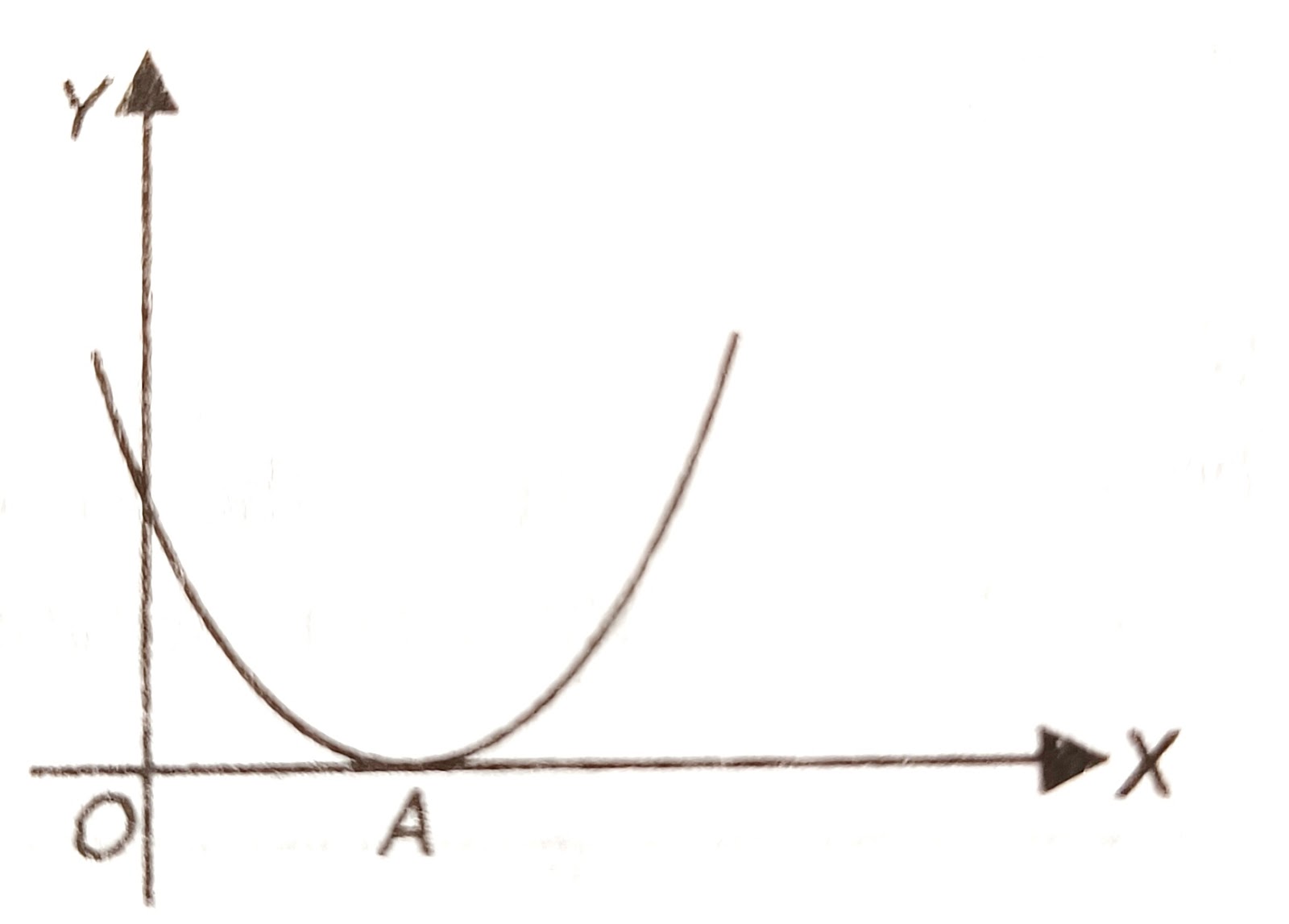
Ex: The two roots x= -5,-5 of the equation (x +5)²= 0 is the x-intercepts of the graph of y= (x +5)² as shown
In this case the vertex of the graph cuts the x-axis at only one point because the roots are equal. In the formula the part b²- 4ac = 0
Ex: The two roots of the equation x²- 2x +2=0 are 1+ i and 1- i. Therefore the graph of the function f(x)= x²- 2x +2 does not touch the x-axis as shown below because the roots are imaginary.
In this case in the formula the part b²- 4ac < 0
Ex: i) Draw a graph of y= x²- 4x +3 for -2≤ x≤ 5.
ii) Use the graph to solve the equation x²- 4x +3=0.
The table of values is
x: -2 -1 0 1 2 3 4 5
y: 15 8 3 0 -1 0 3 8
To solve the equation it is necessary to find the values of x when y=0, i.e., where the graph crosses the x-axis. These points occur when x= 1 and x= 3, therefore these are the solutions.
Sign of the quadratic function ax²+ bx + c, where x ∈ R.
Since the discriminant D= b²- 4ac of ax²+ bx + c =0 can be positive, zero, or negative, we shall examine what sign of the expression ax²+ bx + c would be in these three cases.
Let α, β be the roots of the equation ax²+ bx + c=0. Then ax²+ bx + c ≡ a (x - α)(x - β).
Three cases arise:
Case I: b²- 4ac is negative (D< 0), i.e., when the roots are complex.
We have
ax²+ bx + c= a(x²+ (b/a) x + c/a) Step I. Taking out the coefficient of x².
= a[(x + b/2a)² - (b²- 4ac)/4a²]. Step II. completing the square.
As b¹- 4ac is negative, so -(b²- 4ac)/4a² is positive and (x + b/a)² is also positive for real values of x.
Therefore, the expression has the same sign as a.
Case II: b²- 4ac =0 (D= 0), i.e., when the roots are real and equal (α = β)
ax²+ bx + c= a(x - α)²= a x a positive expression.
Hence, the expression has the same sign as a.
Case III: b²- 4ac is positive (D> 0), i.e., when the roots are real and unequal.
In this case the roots are real and unequal. Let α > β.
i) We assume that x does not lie between α and β. Then,
If x> α, (x - α) and (x - β) β both will be positive. fig 3.08(i)
If x< β, (x - α) and (x -β) both will be negative. fig 3.08(ii)
So, the product (x - α)(x - β) will always be positive.
So, ax²+ bx + c ≡ a(x -α)(x - β) ≡ a x a positive expression.
Hence, the expression has the same sign as a.
ii) If x lies between α and β, then (x - α) and (x - β) will be of opposite signs .
So, The product (x - α)(x - β) will be negative.
So, ax²+ bx + c = a x a is negative expression.
So, ax²+ bx + c and a will be of opposite signs.
From the above discussion it follows that the sign of the expression ax²+ bx + c is always the same as that of a, except when the roots of the equation ax²+ bx + c = 0 are real and distinct and x lies between them.
Values of x Less than β between α & β greater than α
sign of f(x) same that of a opposite to that of a same as that of a
Tests:
i) A quadratic ax²+ bx + c is positive for all real x of a> 0 and D< 0
ii) A quadratic ax²+ bx + c is negative if a< 0 and D< 0.
illustrations
1) The sign of x²+ 6x +12 is positive for real X since D= b²- 4ac = 36 - 47 < 0 and a= 1> 0.
2) The sign of -3x²+ 5x -12 is -ve for all real x since D= b²- 4ac = 25 -4(-3)(-12) = -119< 0 and a= -3< 0
Ex: Find the sign of 6x²- 5x +1 for all real values of x.
D= b²- 4ac = 5²- 4x 6x 1= 1, is positive.
So, the roots are real and different.
By solving the equation, the roots are : 1/2 and 1/3.
So, the given expression has the same sign as the coefficient of x².
i.e., positive for all real values of x except for those which lie between 1/3 and 1/2.
Ex: Determine the sign of the function 3x²- 2x +1 for real values of x.
3x²- 2x +1= 3(x²- (2/3)x + 1/3)
= 3{(x - 1/3)²+ 1/3 - 1/9} {completing the square}
= 3{(x - 1/3)²+ 2/9}
As x is real, the term (x - 1/3)² is always non negative, and hence the function is positive for all real values of x.
Method II
D= b²- 4ac = (2)²- 4(3)(1)= -8.
Therefore, the roots of 3x²- 2x +1=0 are imaginary. Hence 3x²- 2x +1 has the same sign as 'a', i.e., 3, i.e., positive (Case I)
Ex: Find the ranges of the values of x for which x²- 4x +2 lies between -1 and +1.
x²- 4x +2> -1 => x²- 4x +3> 0.
Since the coefficient of x² is positive and the roots of x²- 4x +3=0 are 1 and 3, therefore,
x²- 4x +3> 0 for x < 1 or x> 3* .....(1)
Again, x²- 4x +2< 1 => x²- 4x +1< 0
* Since the coefficient of x² is positive and the roots of x²- 4x +1=0 are 2- √3 and 2+ √3, therefore x²- 4x +1< 0, for 2-√3< x < 2 + √3. ....(3)
Combining (1) and (2) we get 2- √3 < x < 1 or 3< x < 2 +√3.
which are required ranges of the values of x.
Ex: Determine the values of 'a' so that the expression x⅖- 2(a+ 1)x +4, x ∈ R is always positive.
Given: x²- 2(a +1)x +4> 0 for all x.
Since coefficient of x²= 1 is +ve, therefore, sign of x²- 2(a +1)x +4 is positive if D< 0.
i.e., if 4(a+ 1)²- 16< 0,
=> (a+ 1)²- 2²< 0
=> [(a+ 1) +2] [(a +1)-2]< 0
=> (a+3)(a -1)< 0
=> {a - (-3)}(a -1)< 0
=> -3< a< 1 => a ∈ (-3,1)
Note on use a brackets for open and closed intervals.
Sometimet the domains of variation, i.e., the intervals are donated as follows:
i) a< x <b is denoted by (a,b) and is called an open interval of the variable x.
ii) a≤ x ≤ b is denoted by [a,b] and is called a closed interval of the variable x, as x can take up values 'a' and 'b' also.
iii) Any 'x' is denoted by (-∞, ∞). Here, it should be noted that the symbols -∞, ∞ are not numbers in any sense whatsoever .
iv) x≥ a is denoted by [a, ∞), x ≤ b is denoted by (-∞, b).
v) a≤ x < b is denoted by [a, b], a< x ≤ b is denoted by (a,b). These are called semi closed intervals.
αβ ∞