EXERCISE-A
1) Find the area of the triangle whose sides are
a) 3,4,5 cm respectively. 6cm²
b) 30m 40m 50m. 60m²
c) 42cm, 34cm, 20cm. 336cm²
d) 13cm, 14cm, 15cm. 84cm²
e) 30cm, 24cm, 18cm. 216cm²
f) 36cm, 48cm, 60cm. 864cm²
g) 26cm, 28 cm and 30 cm. 336cm²
h) 21cm, 17cm and 10cm. 84cm²
i) 17cm, 25cm and 26cm. 204cm²
j) 52cm, 60cm and 56cm. 1344cm²
k) 42cm, 39cm and 45 cm. 756cm²
2) Find the area of the triangle If:
a) base= 24cm, height= 15cm. 180 cm²
b) base= 15cm, height= 9.6cm. 72cm²
c) base= 2m, height= 15cm. 0.15m²
d) base= 40cm, height= 10cm. 200cm²
3) Find the area of a right angled triangle if its
a) base 24 cm, perpendicular 7cm. 84cm²
b) base 6cm, hypotenuse 10cm. 24cm²
c) perpendicular 60cm and hypotenuse 61cm. 330cm²
4) If one side of a triangle is 24.5cm and the corresponding altitude is 12 cm. Find its area. 147cm²
5) Find the area of a triangle whose base is 8cm and height is 11cm. 44cm²
EXERCISE - B
1) Find the base of the triangle if:
a) Area= 100cm², height= 10cm. 20cm
b) Area= 284cm², height= 71cm. 8cm
c) Area= 336cm², height= 70cm. 9.6cm
d) The area of a triangle is 196cm². Find the length of the base if the corresponding height is 14cm. 28cm
2) Find the height of the triangle if:
a) Area= 500cm², base = 25cm. 40cm
b) Area= 10m², base= 10cm. 20cm
c) Area= 576m², base=24m. 24m
d) Area= 555m², base= 20m. 55.5m
e) The area of a triangle is 216cm². One side of the triangle measure 24cm. Find the distance of the corresponding vertex from the side. 18cm
f)
EXERCISE - C
1) Find :
a) The height on longest side whose sides are 3cm,4cm,5 cm respectively. 2.4cm
b) The height on shortest side whose sides are 3cm,4cm,5cm respectively. 4cm
c) The height on longest side whose sides are 30m,40m,50m respectively. 2.4 m
d) The height on shortest side whose sides are 30m,40m,50 m respectively. 4m
c) The height on longest side whose sides are 42cm, 34cm, 20cm respectively. 16cm
d) The height on shortest side whose sides are 13cm,14cm,15cm. 168/13 cm
e) The height on longest side whose sides are 30cm, 24cm, 18cm. 14.4cm
f) The height on shortest side of the triangle whose sides are 36cm, 48cm, 60cm respectively. 48cm
g) Find the area of a triangle of sides 13cm, 14cm and 15cm. also, find the length of the perpendicular from the vertex opposite the side of length 14cm. 84cm², 12cm
EXERCISE - D
1) Find the area of an equilateral triangle of side
a) 4 cm. 6.93cm²
b) 5cm. 10.83cm²
c) 7cm. 21.22cm²
Correct to two decimal places .
d) Find the area of an equilateral triangle of side 6cm, correct to 3 places of decimal. 15.588 cm²
e) If the area of an equilateral triangle is 64√3cm². Then find its side. 16cm
2)a) If the area of an equilateral triangle is 36√3cm², find the length of its side and its perimeter. 12cm, 36cm
b) If the area of an equilateral triangle is 25√3m², find its perimeter and altitude correct to 3 significant figures. 30m, 8.66m
c) Find the perimeter of an equilateral triangle of area 16√3. 24m
d) If the ratio of the base and the hypotenuse of a right angled triangle is 4:5. and the perimeter of the triangle is 48cm, find its area. 96 cm²
EXERCISE--2
1) Find the two perpendicular sides of a right angle whose hypotenuse is 20cm and the area is 96 cm². 16, 12cm
2) In a right angled triangle ABC, right angled at B, the altitude from B to AC intersects AB at D. If AD= 8cm, and AC =12cm, find BD. 4√2 cm
3) The base of a right angled triangle is 7cm and its area is 84 cm². Find its hypotenuse. 25
4) In a right angled triangle ABC, find the height of the altitude BD drawn from B to the hypotenuse AC, given AB= 9cm and BC= 12cm. 7.2cm
5) ABC is a triangle in which D is the midpoint of the side BC and E is the midpoint of AD. What is the ratio of the areas of∆ BED anf ∆ABC. 1:4
6) In ∆ABC, AD is the perpendicular to BC. If AB= 10, AC= 17. Find the value of AD and CD. 8, 15
7) A ad B leaves a point at the point at the same time. A travels North at 18km/hr and B travels West at a speed of 24 km/hr. Find the distance between A and B after two hours. 60 km
8) If the diagonal of a square is 8cm, then find the side of the square. 4√2.
9) A right angled triangle at B. Side AB= 3 and hypotenuse AC= 5 find the perpendicular BD on side AC. 4
10) The perimeter of a square is equal to the perimeter of an equilateral triangle. Find the ratio of the side of the equilateral triangle to the diagonal of the square.
11) The perimeter of a right angled triangle is 90cm and its area is 270 cm². Find the length of the hypotenuse. 39
12) Find the area of an Isosceles triangle whose equal sides measure 20cm each and base measure 24cm. 192
13) A triangular piece of land is divided between two brothers equally. What is the length of the shortest wall that can be build between their plots, if the length of the sides of the plot are 20m, 21m, 29m. 10√2
14) ∆ PQR is equilateral and PO, QM, RL are the altitudes LR²+ QM²+ PO²= 51√3 cm², find the area of ∆ PQR. 17cm²
15) Two poles of height 6m and 11m stand vertically upright on a plane ground. If the distance between their foot is 12m, find the distance between their tops. 13cm
16) In a right angled triangle, find the hypotenuse if base and perpendicular are respectively 36015 and 48020cm. 69125
17) In a Quadrilateral ABCD, AD= 20, CD= 20, BC= 12 & diagonal AC= 20. Angle B is 90°. Find the area of the Quadrilateral. 269
18) The sides of a triangle are 21, 20 and 13cm. Find the area of the larger triangle into which the given triangle is divided by the perpendicular upon the longest side from the opposite vertex. 96 cm²
DIAGRAMMATIC QUESTIONS
1) Find the area of ∆ triangle ABC
2) In the adjoining diagram, Find the area of the triangle
Also , find the length of the perpendicular drawn from the vertex opposite the side of the length 36cm. 360cm², 20cm
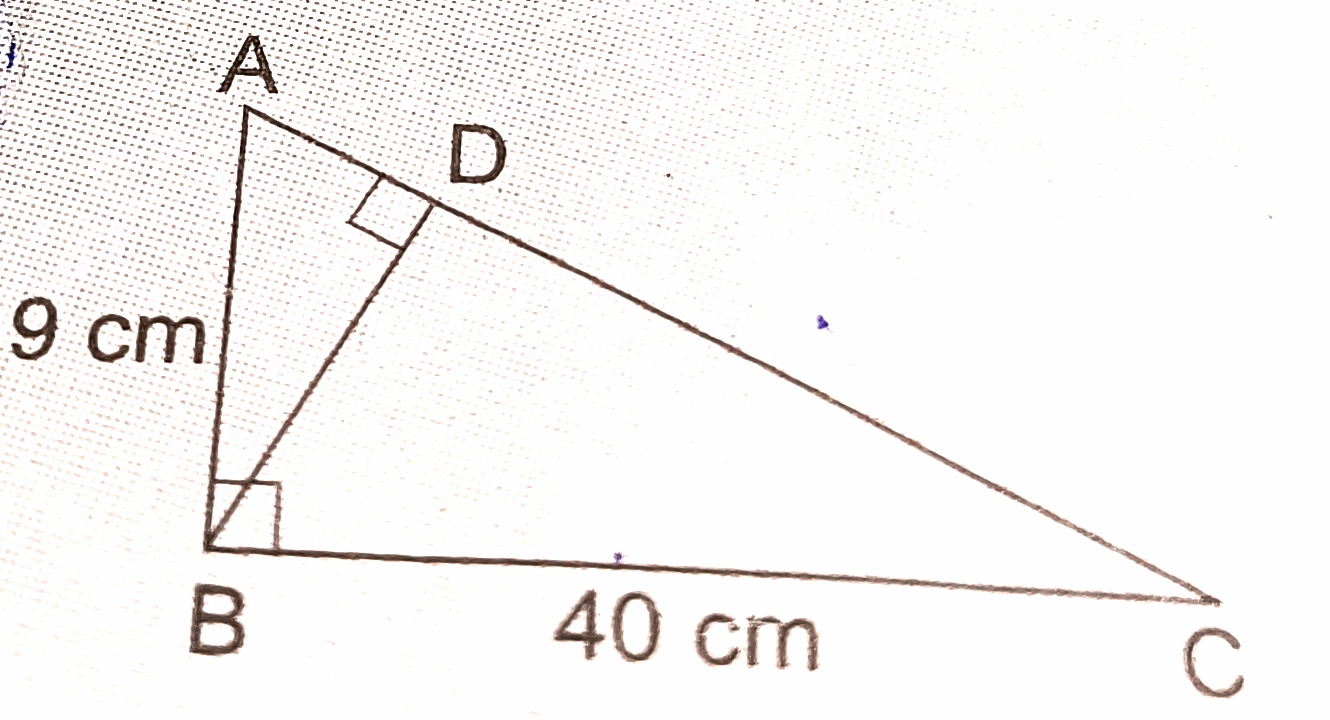
3) In the figure, ABC is a right angled triangle.
a) area of ∆ ABC. 180cm²
b) the length of AC. 41cm
c) the length of BD correct to two decimal places. 8.78cm
4) Find the area of the shaded region in each of the following figures. in which the dimension given are in cm
a)
b) 217.70cm²
c) 72cm²





No comments:
Post a Comment