TRIANGLEA triangle is a closed curves formed by three line segments. 'Tri' means 'three'. A triangle is 3 sides, 3 angles in 3 vertices.
The adjoining figure shows a triangle ABC. The line segments AB, BC and CA are called its
sides. The angles A, B and C are called its
interior angles or simply
angles. The points A, B and C are called its
vertices. Three sides and the 3 angles are called its 6
elements.In the above figure, vertex A. It is the point of intersection of the sides AB and AC, BC is the remaining side. Vertex A and side BC are opposite to each other. Also angle A and BC are opposite to each other.
Similarly, vertex B and side CA are opposite to each other; angle B and side C are opposite to each other. Same can be said about vertex C, angle C and side AB.
Types of triangles
Types of triangles on the basis of sides.
a) Scalene triangle. If all the sides of a triangle are unequal , it is called Scalene triangle.
In the adjoining figure AB≠ BC ≠ CA, so ∆ABC is a scalene triangle.
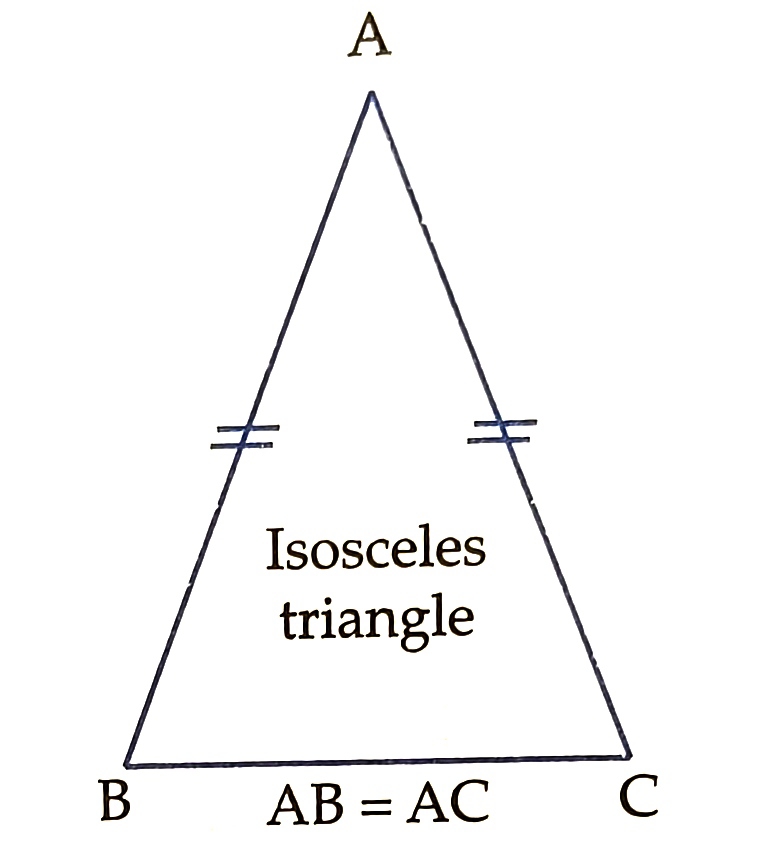
b) Isosceles triangle: If any two sides of a triangle are equal , it is called an Isosceles triangle.
In the figure AB= AC, so ∆ABC is an Isosceles triangle. Usually equal sides are indicating by putting you marks on each of them.
c) Equilateral triangle: If all the three sides of a triangle are equal, it is called an equilateral triangle .
In the figure AB = BC = AC, so ∆ABC is an equilateral triangle.
Types of triangles on the basis of angles.
a) Acute angle triangle : If all the three angles of a triangle are acute( less than 90°), it is called acute angle triangle.
In the adjoining figure, each angle is less than 90°, so ∆ABC is an acute angled triangle.
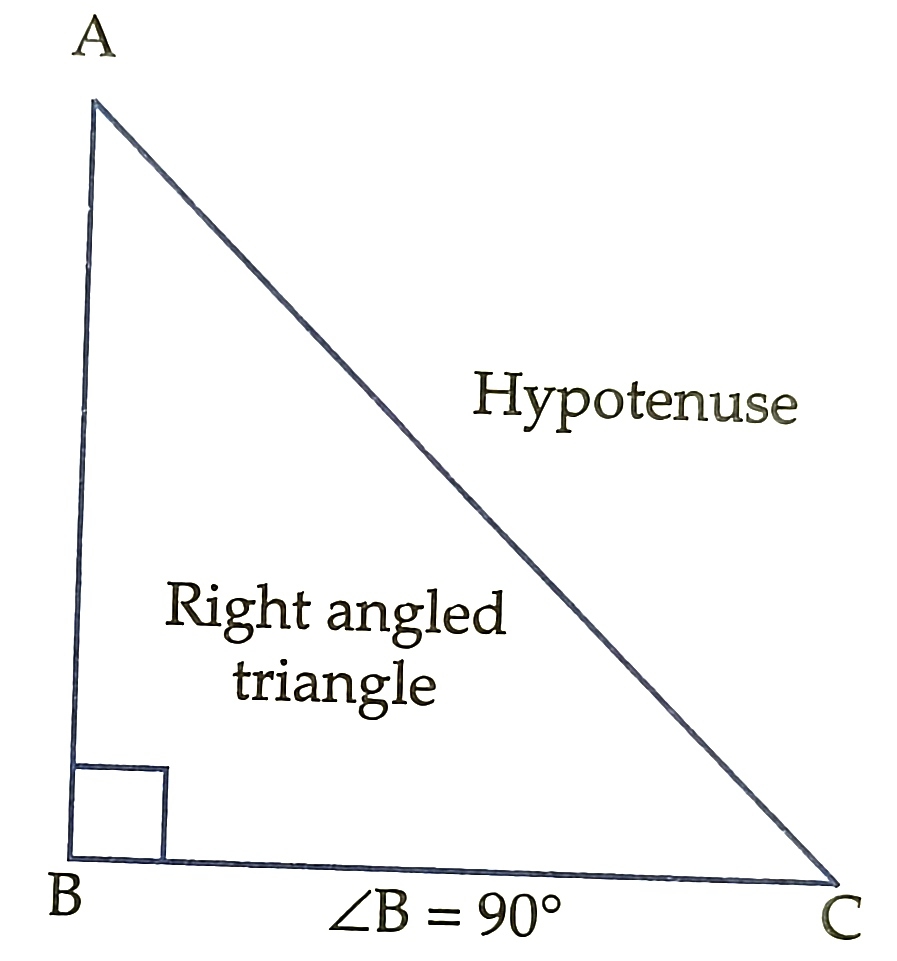
b) Right -angled triangle. If one angle of a triangle is a right angle(= 90°), it is called a right angled triangle.
In a right angled triangle, the side opposite to right angle is called hypotenuse.
In the adjoining figure, angle B=90°, so ∆ABC is a right angled triangle and side AC is the hypotenuse.
c) Obtuse angled triangle: If one of a triangle is obtuse( greater than 90°), it is called an obtuse angle triangle.
In the adjoining diagram, angle B is obtuse( greater than 90°), so ∆ABC is an obtuse angled triangle.
Some Terms Connected With A Triangle
Orthocentre : Perpendicular from a vertex of a triangle to the opposite side is called an altitude of the triangle.
In the adjoining figure AD perpendicular to BC, so AD is an altitude of ∆ABC.
A triangle has 3 altitudes
In fact, all the three altitudes of a triangle pass through the same point and the point of concurrence is called the orthocentre of the triangle.
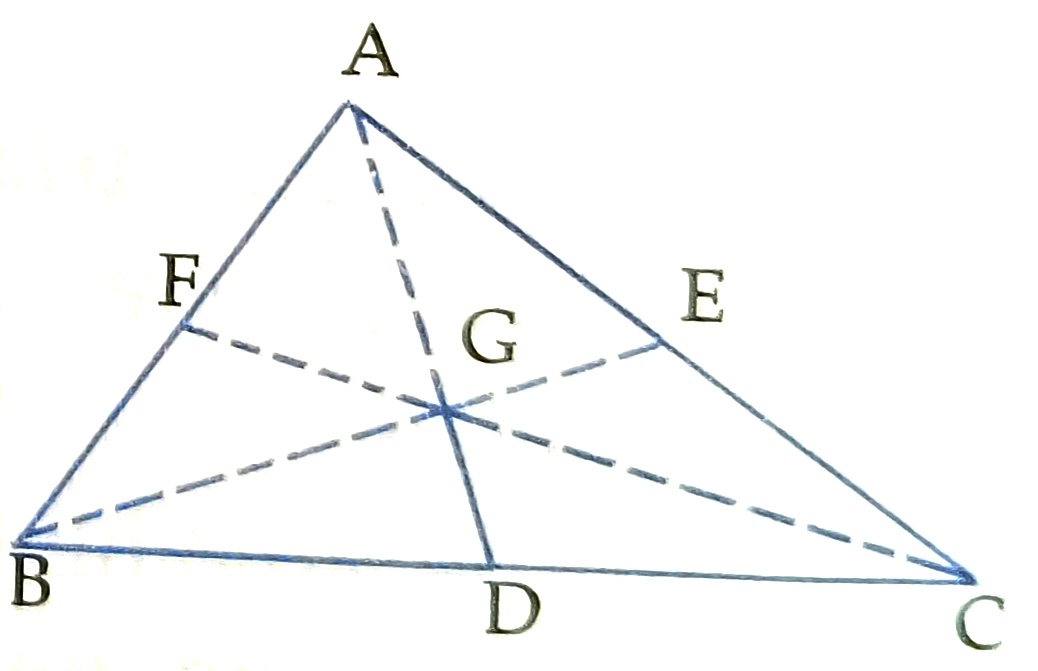
Centroid : The straight line joining a vertex of a triangle to the mid-point of the opposite side is called the median of the triangle.
In the adjoining figure, D is midpoint of BC, so AD is a median of ∆ABC.
In fact, all the three medians of the triangle pass through the same point and point of concurrence is called the centroid of the triangle.
The centroid of a triangle divides every medium in the ratio 2 :1. Thus, if G the centroid of ∆ABC, then
AG: GD= 2:1, BG: GE = 2 : 1 and CG: GF = 2:1.
Incentre and Incircle
Line bisecting an (interior) angle of a triangle is called the (internal) bisector of the angle of the triangle.
In the adjoining figure, angBAI= angIAC, so AI is the (internal) bisector of angle A.
A triangle has three internal bisectors of its angles.
In fact, all the three( internal) bisectors of the angles of a triangle pass through the same point and the point of concurrence is called the incentre of the triangle.
In the above figure, IA, IB, and IC are the (internal) bisectors of angle A, B and C respectively. so I is the incenter of ∆ABC.
Moreover, incentre is the centre of a circle which touches all the sides of ∆ABC and this circle is called incircle of ∆ABC.
Circumcenter and Circumcircle
Line bisecting a side of a triangle and perpendicular to it is called the right bisector of the side of the triangle.
In the adjoining figure, D is midpoint of BC and CD is perpendicular to BC, so OD is the right bisector of the side BC.
A triangle has 3 right bisectors of it sides.
In fact, all the three right bisectors of the sides of a triangle pass through the same point and the point of concurrence is called the circumcenter of the triangle.
In the adjoining figure, OD, OE, OF are the right bisectors of the sides BC, CA and AB respectively of ∆ABC. so O is the circumsenter of ∆ ABC.
Moreover , circumcenter is the centre of a circle which passes through the vertices of ∆ABC and this circle is called circumcircle of ∆ABC.
The sum of angles of a triangle is 180°
In the adjoining figure AngA+ angB+ angC=180°.
An exterior angle property of a triangle
Let ABC be a triangle and its bisect BC be produced to D, then angACD is called an exterior angle at C. The two interior angles of the triangle that are opposite to the exterio angACD are called its interior opposite angles or remote interior angles. Thus, angABC and angBAC of ∆ABC are interior opposite angles of the exterior angleACD.
An exterior angle of a triangle is equal to the sum of the interior opposite angles.
In the figure, angACD = angA+ angB.
CONGRUENCE OF TRIANGLES
Two triangles are called congruent if and only if they have exactly the same shape and the same size.
a) congruent triangles are 'equal in all respects ' i.e., they are the exact duplicate of each other.
b) If two triangles are congruent, then any one can be superposed on the other to cover it exactly.
c) In congruent triangles, the sides and the angles which coincide by superposition are called the corresponding sides and corresponding angles.
d) The corresponding sides lie opposite to the equal angles and corresponding angles lie opposite to the equal sides.
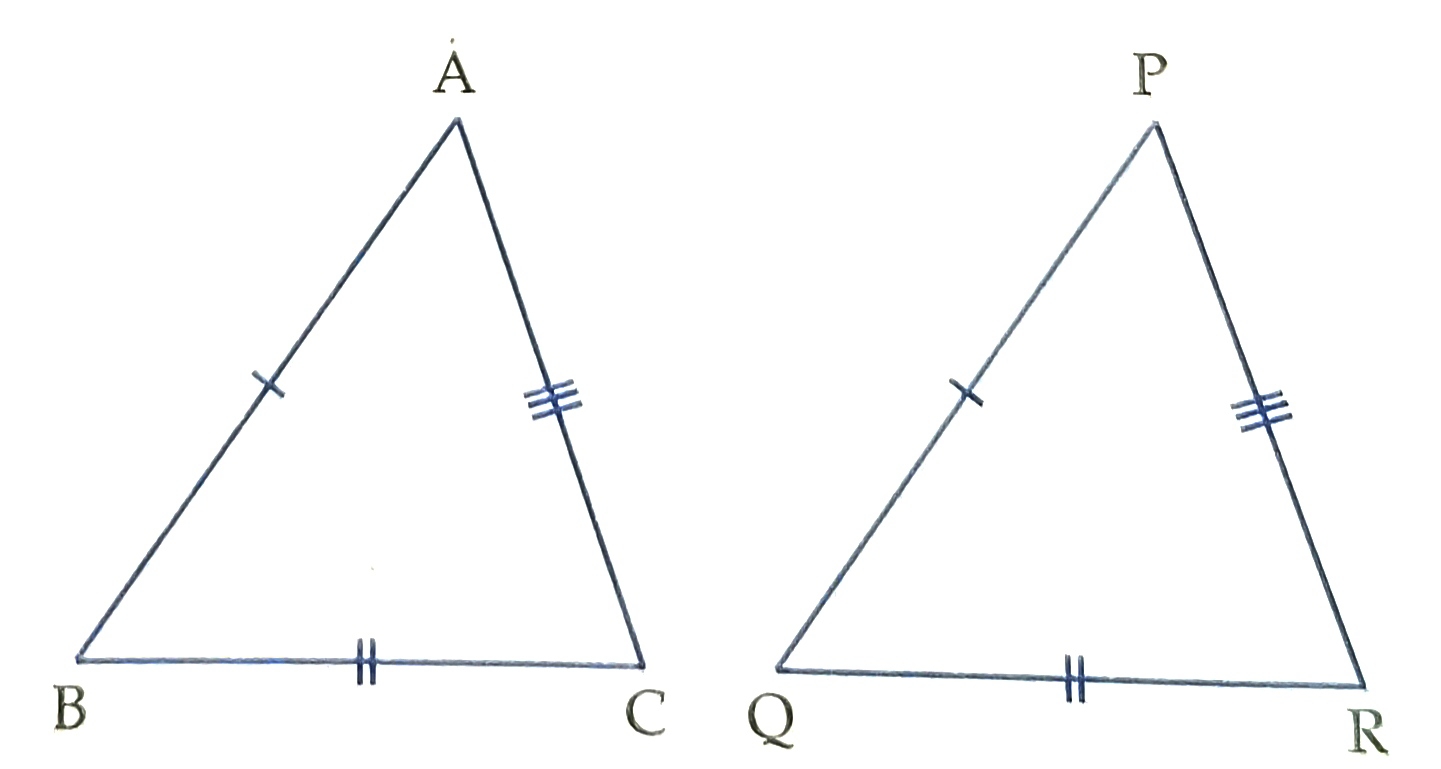
In the adjoining diagram, angA= angP, therefore, the corresponding sides BC and QR are equal. Also BC= QR, therefore , the corresponding angles A and P are equal.
e) The order of the letters in the name of congruent triangles displays the corresponding relationship between the two triangles.
Thus, when we write ∆ABC congruent to ∆PQR, it means that A lies on P, B lies on Q and C lies on R i.e., angA= angP, angB= angQ, angC= angR and BC= QR, CA= RP, AB= PQ.
Exercise -A
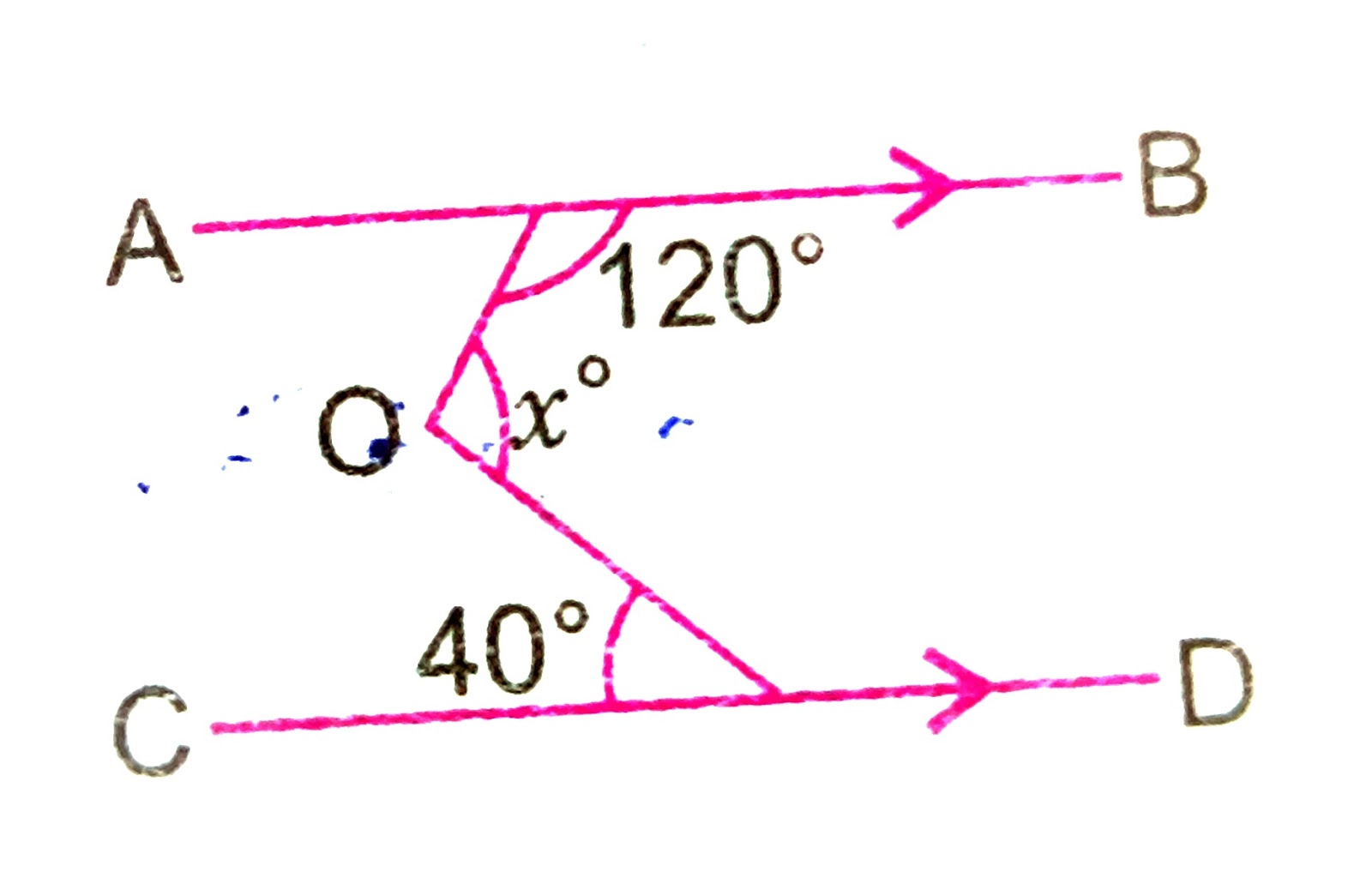
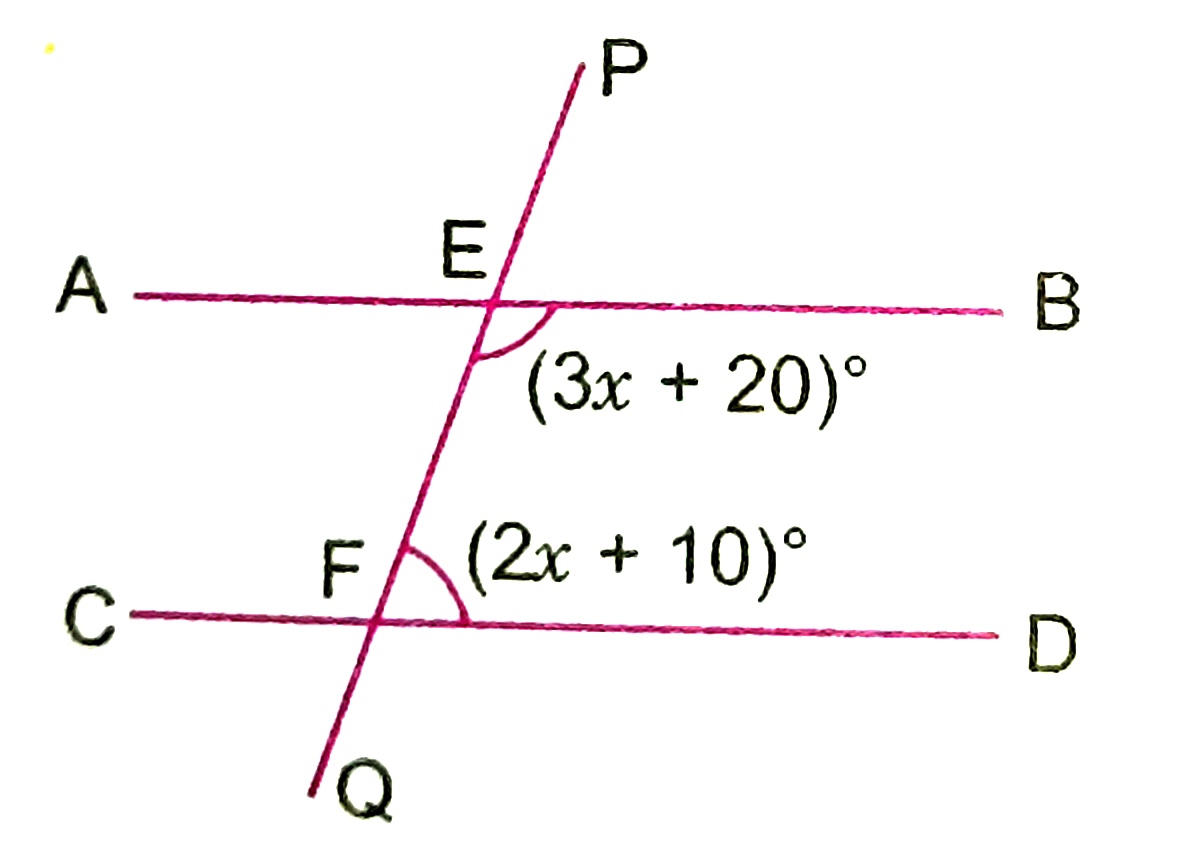
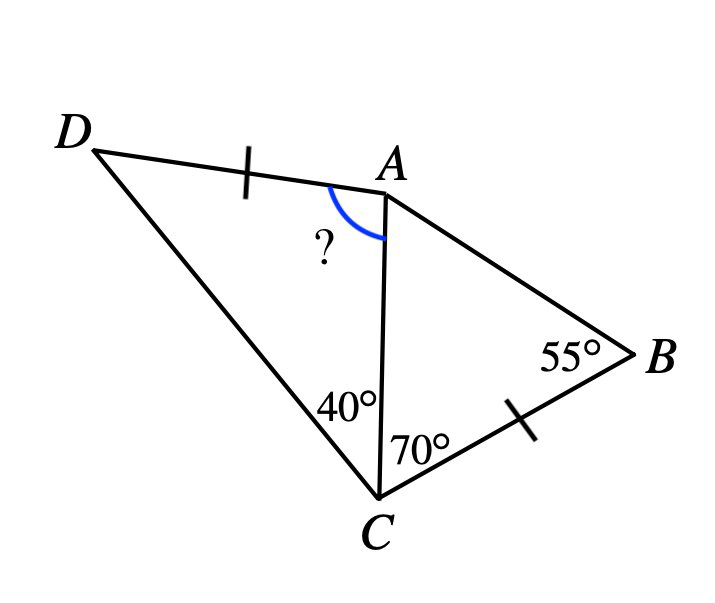
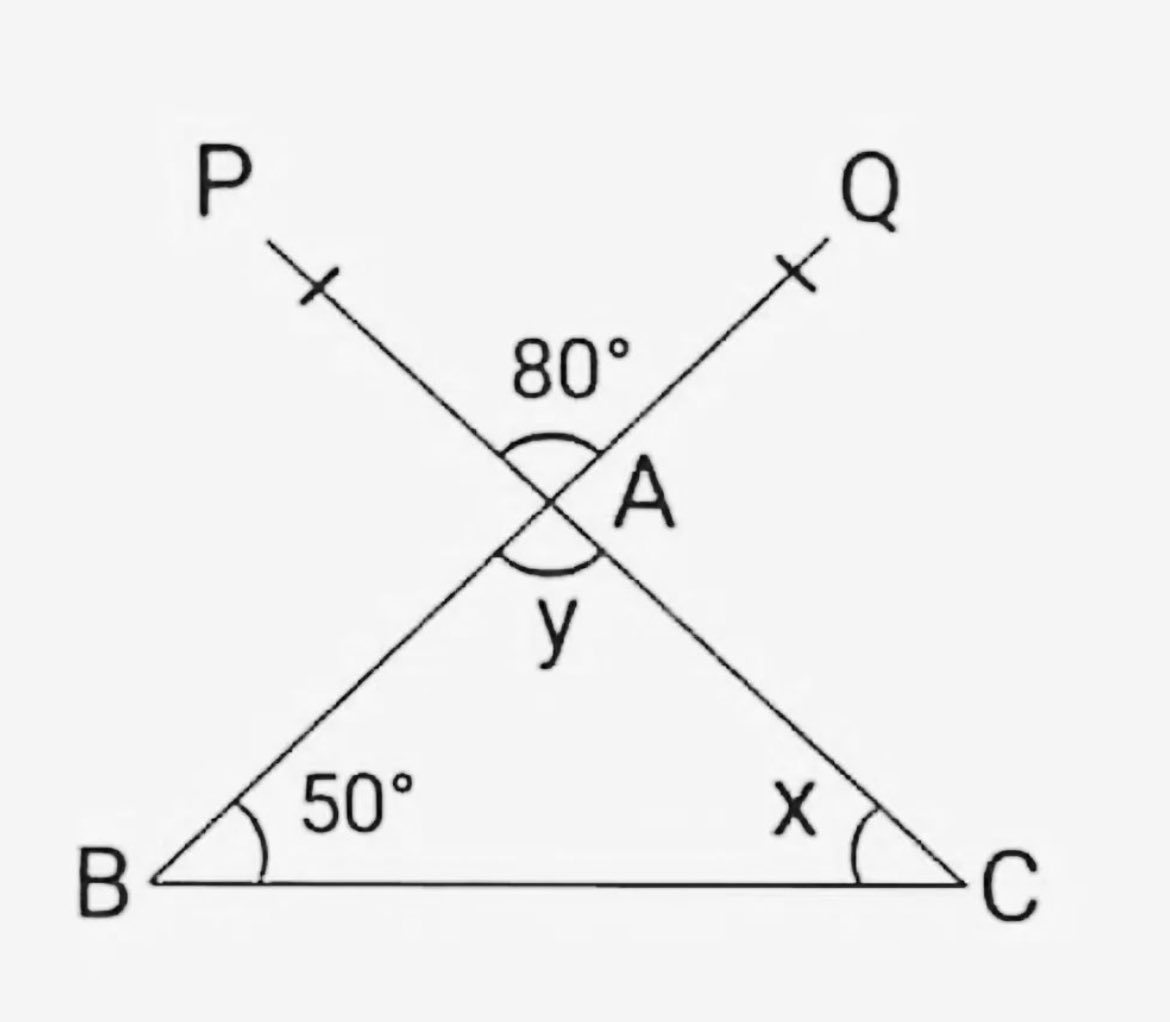
1) In the adjoining figure, find the values of x and y.
2) In the ∆ABC given below,
BD bisects angB and is perpendicular to AC. If the lengths of the sides of the triangle are expressed in terms of x and y as shown,
find the values of x and y.
a) 12,8 b) 16,8 c) 8,12 d) 6,18
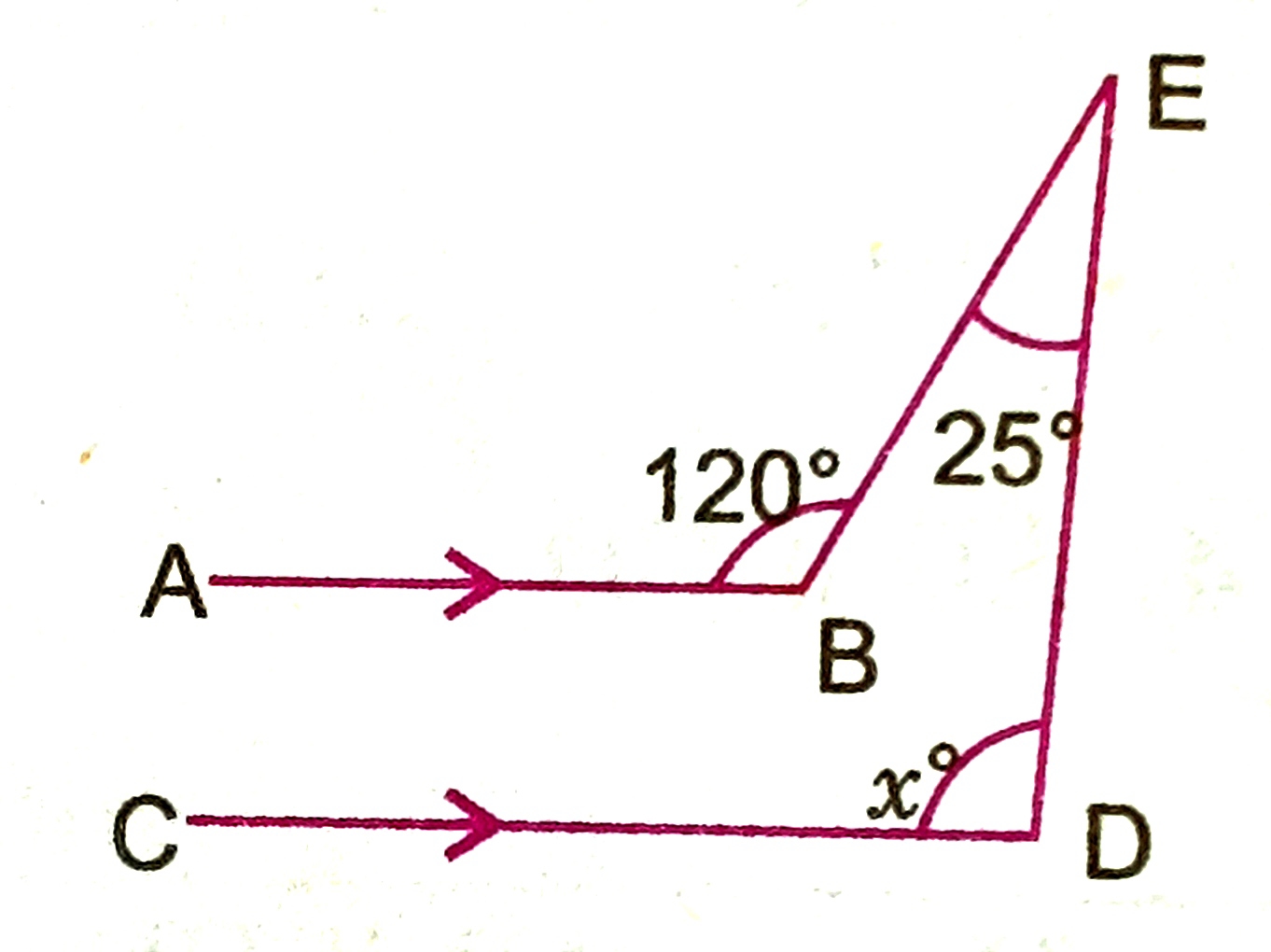
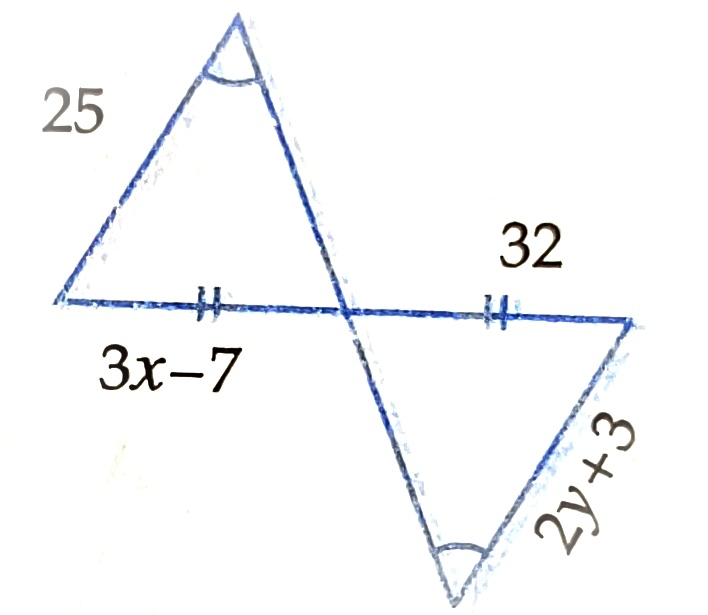
3) Find the value of x and y
a) 10,11 b) 12,11 c) 13,11 d) 14,12
4) Find the value of x and y
a) 8,4 b) 9,5 c) 7,9 d) 10,12
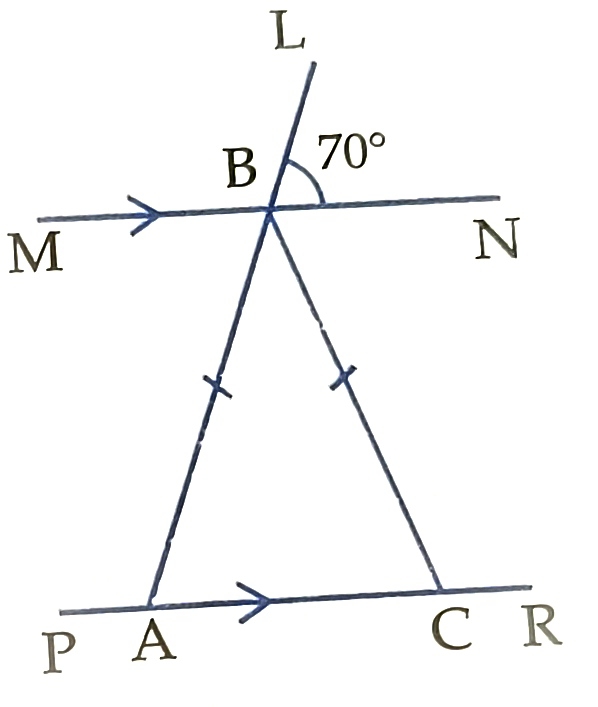
5) In the figure, MN is parallel to PR, angLBN= 70° and AB= BC.
a) 20 b) 40 c) 60 d) 80 e) 90
6) In the joining figure ABC is an isosceles triangle with AB= AC and LM is parallel to BC.
If angA= 50°, Find angLMC.
a) 100 b) 110 c) 115 d) 115
7) In the figure AB= AC, CH= CB and HK|| BC.
If angCAD=137°, find angCHK
a) 40 b) 44 c) 43 d) 54 e) 65
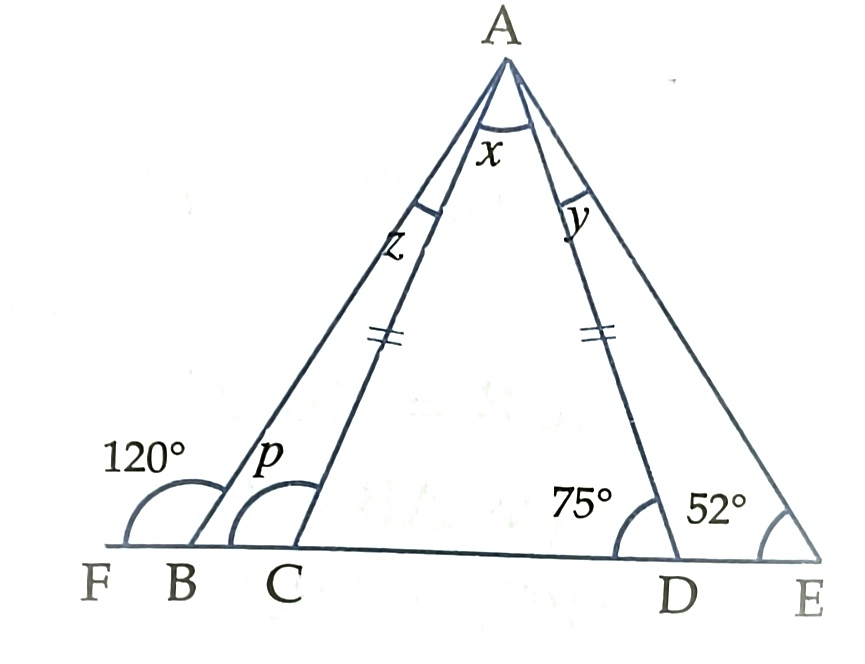
8) Find the measure of each lettered angle in the adjoining figure.
a) 30,23,15,105 b) 30,32,65,90 c) 42,45,65,89 d) none
9) From the given figure,
a) 33 b) 23 c) 32°40' d) none
10) In ∆ABC, AB= AC and D is a point on AB such that AD= DC = BC.
a) 23 b) 34 c) 36 d) 76
11) ABC is a right angled triangle in which angA=90° and AB=AC. Find the angB and angC
a) 45,45 b) 30,60 c) 40,50 d) none
a) 30 b) 120 c) 115 d) 132
a) 24 b) 48 c) 68 d) 74
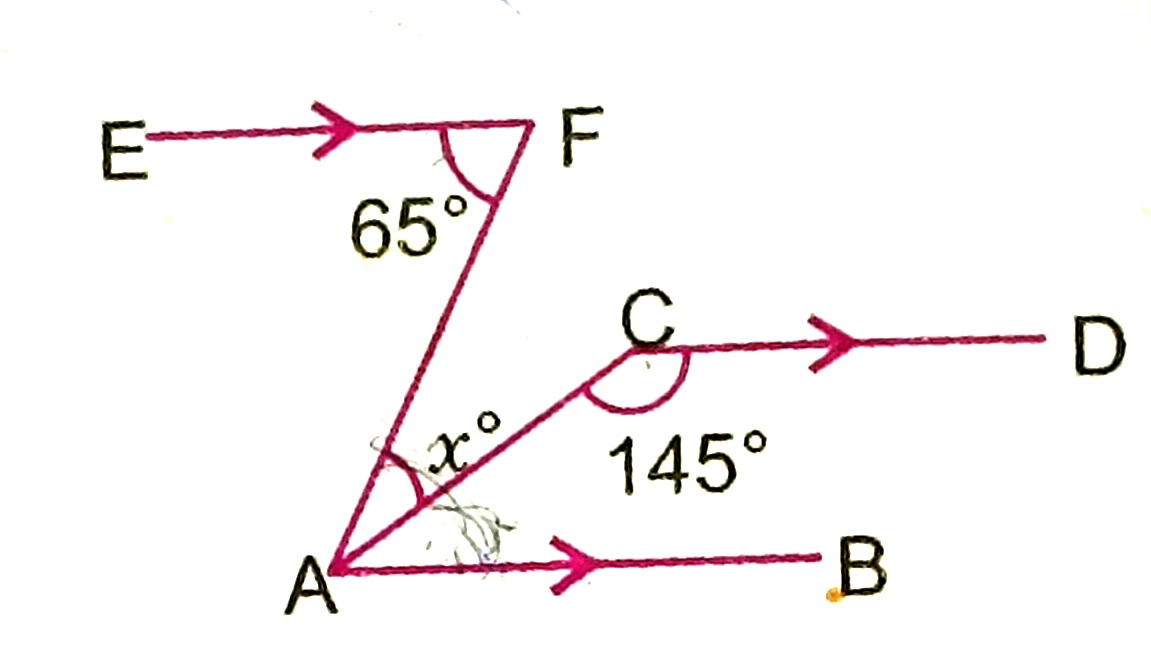
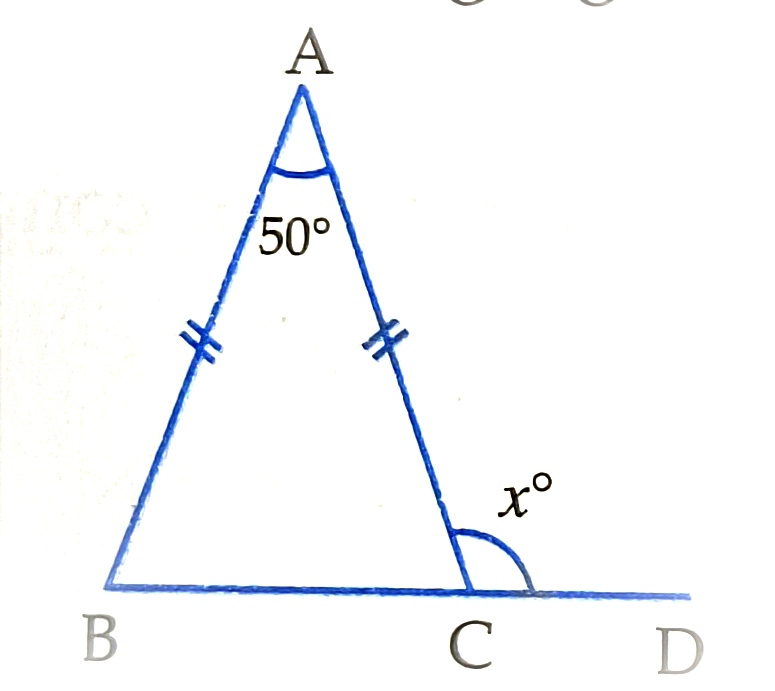
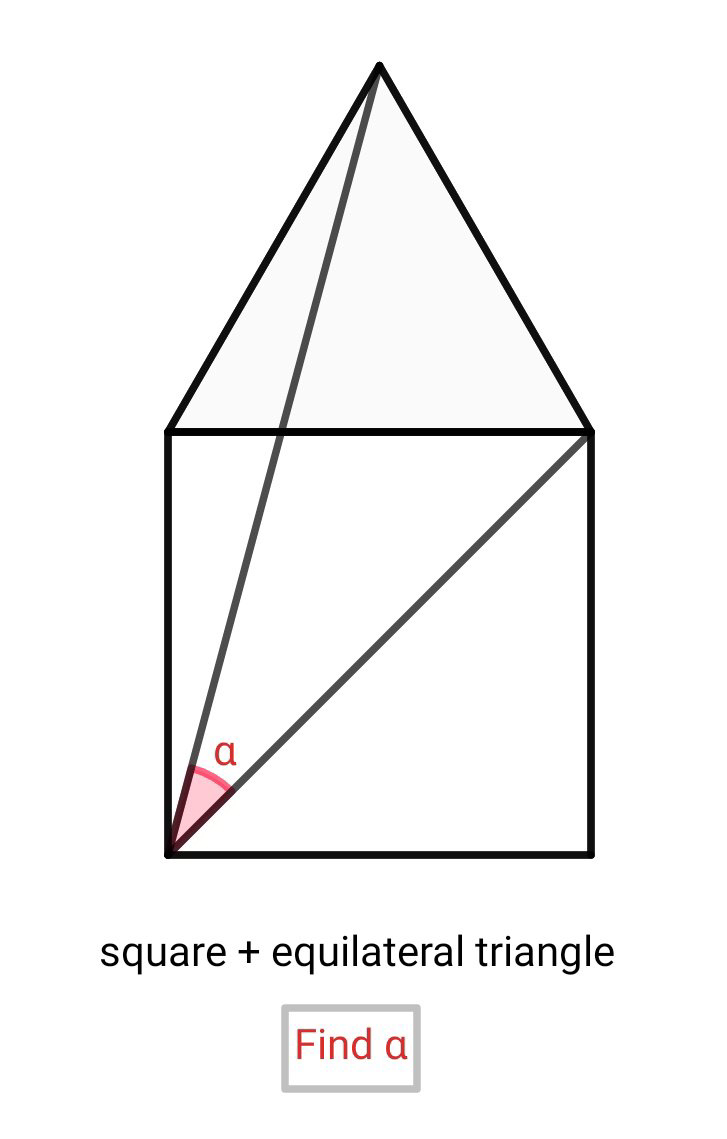
Find x
a) 45 b) 65 c) 72 d) 87
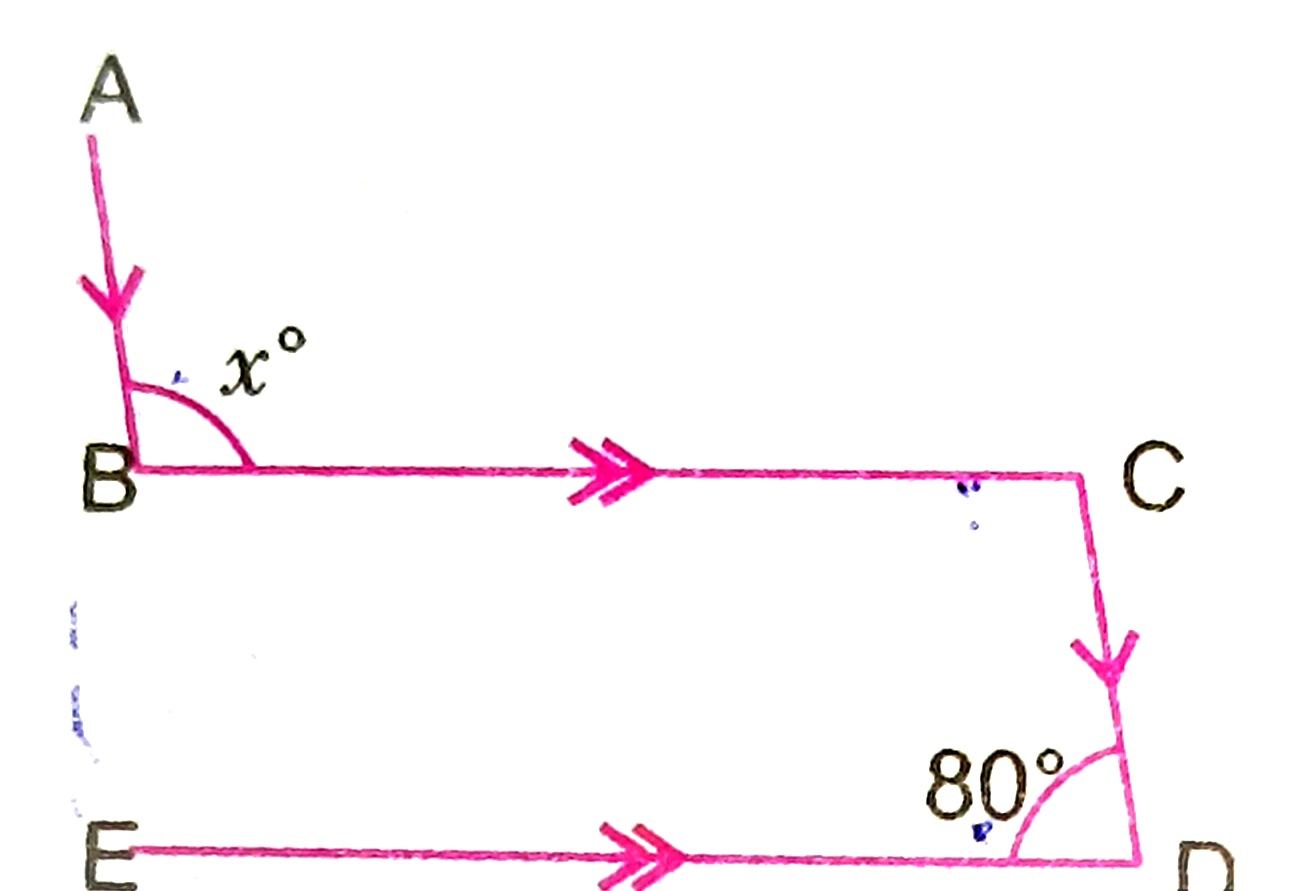
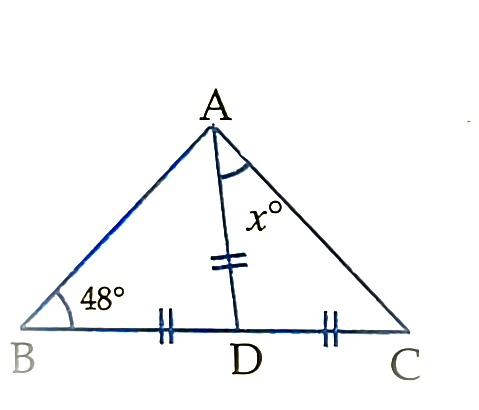
Find x
a) 34 b) 42 c) 45 d) 65
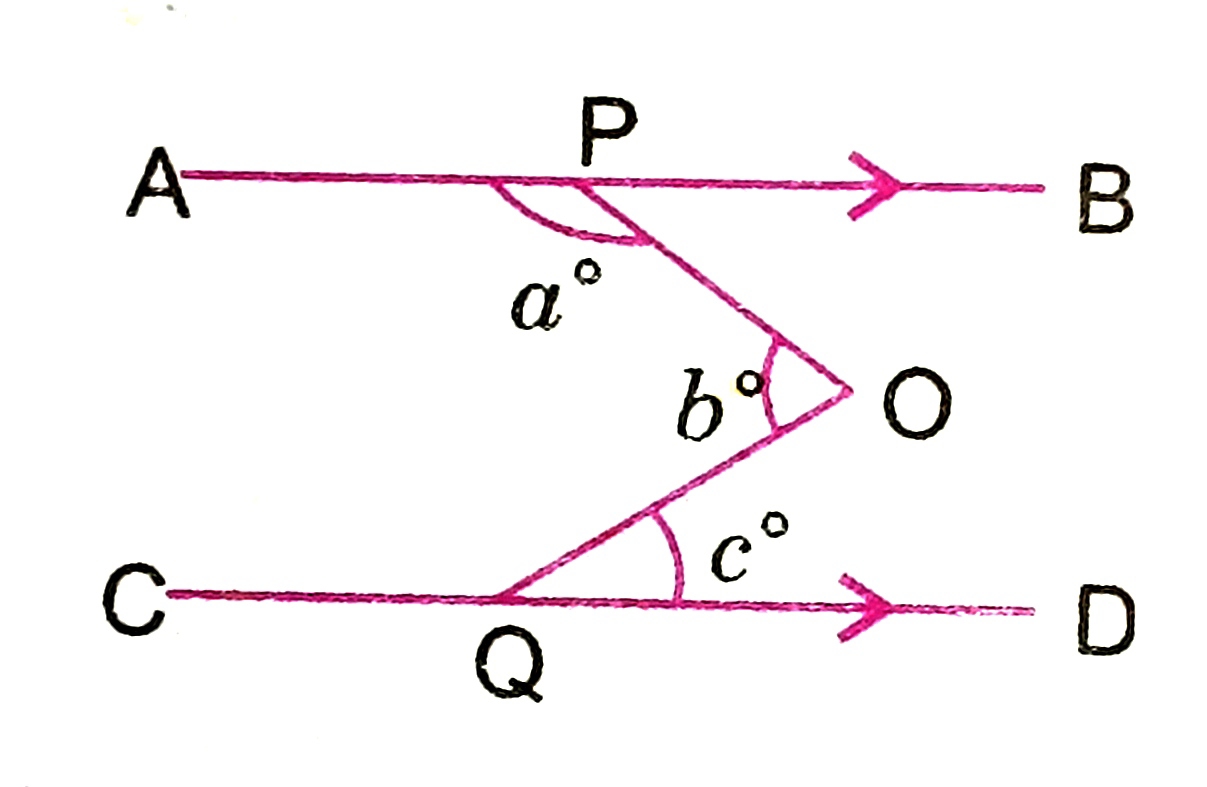
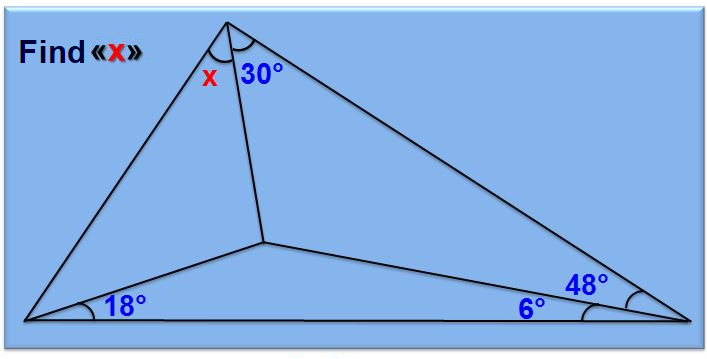
Find the value of x
a) 30 b) 40 c) 76 d) 56
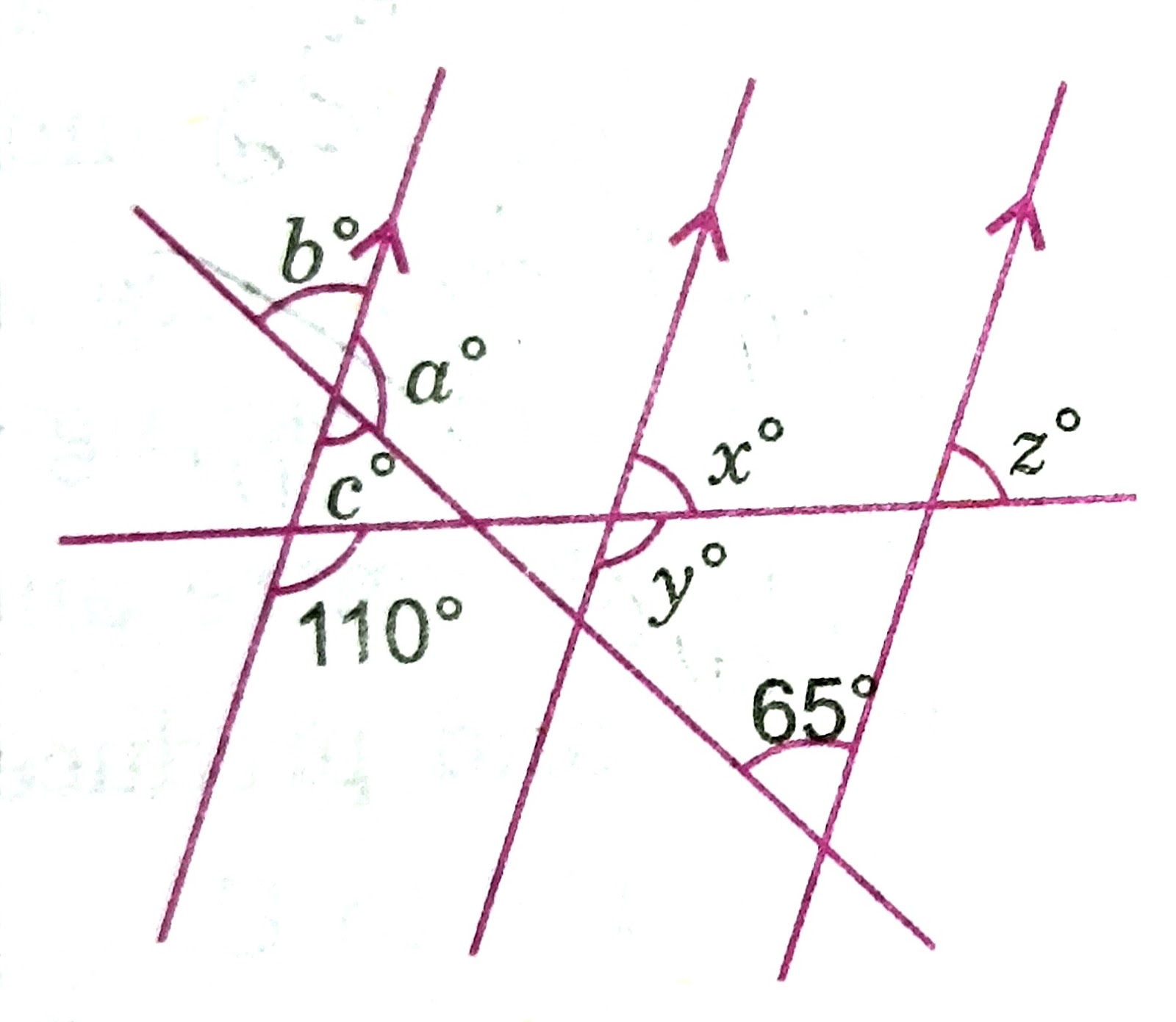
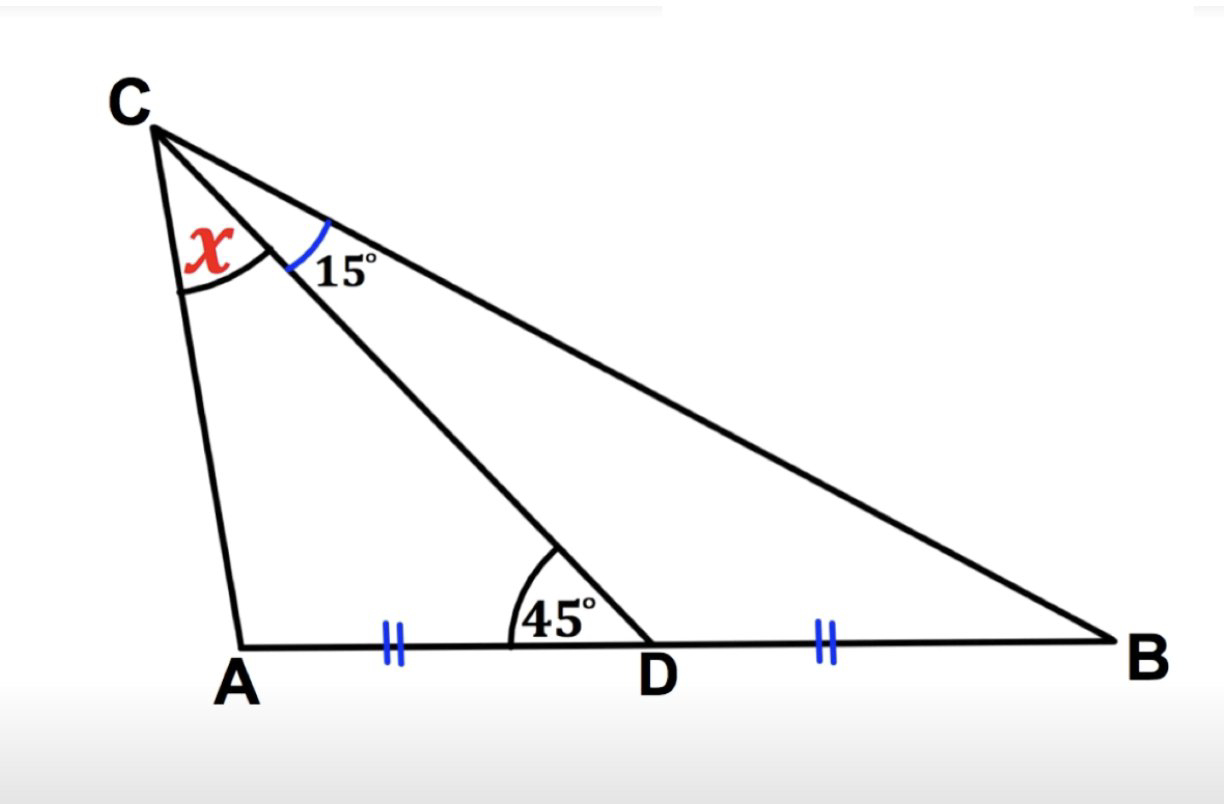
17) Find the value of x
18) In the figure AB= DC, BC= DC.
a) 90 b) 85 c) 102 d) 120
19) In the figure BC= CD
a) 67 b) 74 c) 86 d) 97
20) In the figure AB||CD and CA= CE. If angACE=74 and angBAE= 15.
find the values of x and y
a) 127,38 b) 12,36 c) 100,80 d) none
21) In ∆ABC, AB=AC, angA=(5 x + 20)° and each of the base angle is 2/5th of angA. Find the measure of angA.
a) 90 b) 100 c) 110 d) 120
22) In the figure given below,
ABC is an equilateral triangle. Base BC is produced to E , such that BC= CE. Calculate angACE and ang AEC
a) 12030 b)112, 45 c) 120, 45 d) none
23) In the figure given below
Find the value of angBAD: angADB
a) 1:2 b) 2:1 c) 3:1 d) 3:2
24) In the figure given AB|| CD find the value of x+ y+z
a) 126 b) 136 c) 146 d) 156 e) 166
a) 30 b) 40 c) 65 d) 87 e) none
a) 76 b) 65 c) 82 d) 34 e) none
a) 120 b) 132 c) 45 d) 60 e) none
28) Find the value of ? Marks
a) 35 b) 65 c) 45 d) 60 e) none
a) 55 b) 65 c) 75 d) 85 e) none
a) 100 b/ 120 c) 130 d) 200 e) none
a) 15 b) 25 c) 45 d) 60 e) none
32)
which of the following is not a criterion for congruence of triangle essay is as a s s a s s equals to FC f is equal to BD and AFC CBT then the rule by which triangle is CBD is sasas ab perpendicular to b e ab equals to AC and radius the median of ABC then angle abc is equal to 61 2975 acques to abc DBA then AC is equals to be abc at BD and DM are perpendicular to Owaisi such that bndm ifob5 then BD is 68 and 12 In triangle ABC AB = ACB 50 degree then C is equals to 40 581 30 in triangle abc BC is equals to abba 80 degree then a is equals to 80 405100 triangle pqr is equals to PP QR 4 pr5 in the length of the PQ 4 by 2 2.5 In triangle ABC pqr AB equal to ACP angles are isosceles but not conclude I should use and congruent triangle of length 5 cm and 1.5 CM length of the third side of the triangle cannot be 3.64.13.3.2 what is not possible to construct a triangle when the length of its side sir 678466 5.32.23.19.35.27.2 then the length of the third side is 4:10 740 rules for congruency of two triangles SS 3 sides of one triangle are equal to 3 sides of the other triangle says to sides in the included angle of one triangle are equal to two sides and the included angle of the other triangle as A2 angles and interior side of the one triangle are equal to 2 angle and the included side of the triangle A A is 2 angles and non included side of one triangle are equal to the angles the responding sides of the triangle are equals to the hypotenuse in a triangle the angles of opposite sequel sides are equal in a triangle the sides are positive sides of a triangle side has a greater angle opposite to it equal then the longest sites as a greater angle opposite to it if two angle triangle as a longer side opposite to it the sum of two sides of a triangle is greater than the third side the difference between any two sides of a triangle is less than the third side of all the line segment that can be drawn to a figure line from a point not lying on it the perpendicular line ABCD is a square P q r D points on the side ABC City respectively such that apbq CR and PQ 190 find prq 4569120 36 find the value of x in the figure given below find the value of x in the figure given below absc DBC calculate x y BSE in the figure below calculate the size of each letter angle in the