Type -1
2)) The radius of a circle is 17cm and the length of perpendicular drawn from its centre to a chord is 8.0cm. Calculate the length of the chord. 30cm
3) Find the length of a chord which is at a distance of 6cm from the centre of a circle of radius 12cm. 20.78
4)
5) Find the length of the chord which is at a distance of 5cm from the centre of a circle of radius 10cm. 17.32
6) Find the length of a chord which is at a distance of 4cm from the centre of the circle of radius 6cm. 8.94cm
7) Find the length of a chord which is at a distance of 3cm from the centre of the circle of radius 5cm. 8cm
8) The radius of a circle is 8cm and the length of one of its chords is 12cm. Find the distance of the chord from the centre. 5.291cm
9) Find the length of a chord which is at a distance of 5cm from the centre of a circle of radius 13cm. 24cm
Type-2
1) A chord of length 6cm is drawn in a circle radius 5cm. Calculate its distance from the centre of the circle. 4cm
2) The radius of a circle is 10cm and length of one of its chord is 16cm. Find the distance of the chord from the centre. 6cm
3) the radius of a circle is 8cm and the length of one of its chord is 12cm. Find the distance of the chord from the centre. 5.14cm
4) The radius of a circle 13cm and the length of one of its chords is 10cm. Find the distance of the chord from the centre. 12cm
5) The length of chord and radius is 3 and 1.7. Find the distance of the centre of the circle from the chord.
Type -3
1) A chord of length 8cm is drawn at a distance of 3cm from the centre of a circle. Calculate the radius of the circle. 5cm
2) The length of a chord of a circle is 4cm. If its distance from the centre is 1.5cm, determine the radius of the circle. 2.5cm
Type -4
1) A chord of length 24cm is at a distance of 5cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12cm from the centre. 10cm
Type -5
1) Two parallel chords of lengths 16.0cm and 12.0cm are drawn in a circle of diameter 20cm. Find the distance between the chords , if the both the chords are:
a) on the same side of the centre, 2cm
b) on the opposite sides of the centre. 14
2) In a circle of radius 17 cm, two parallel chords of length 30cm and 16cm are drawn. Find the distance between the chords if both the chords are:
a) on the opposite sides of the centre. 23cm
b) on the same side of the centre. 7cm
3) In a circle of radius 5 cm, there are two parallel chords of length 4cm and 6cm.
Find the distance between them when they are
a) on the same side of the centre.
b) on opposite sides of the centre. (√21-4), (4+√21)
4) PQ and RS are two parallel chords of a circle whose centre is O and radius is 10cm. If PQ =16cm and RS= 12cm,
a) on the same side of the centre O. 2cm
b) on opposite side of the centre O. 14cm
5) a) AB and CD are parallel chords of a circle of radius 5cm. Given that AB= 6cm, CD= 8cm and that the chords AB and CD lie on the same side of the centre O. Calculate the distance between the chords.
6) Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24cm and the distance between the two chords is 21cm; find the length of another chord. 18cm
7) Two chords AB, CD of length 5cm, 11cm respectively of a circle are parallel. If the distance AB and CD is 3cm, find the radius of the circle. 6.04cm
8) Two chords AB, CD of lengths 5cm, 11cm respectively of a circle are parallel. if the distance between AB and CD is 3cm, find the radius of the circle. √146/2
9) AB and CD are 2 chords of a circle on the opposite sides of the centre such that AB= 10cm, CD= 24cm and AB|| CD; the distance between AB and CD is 17cm. Find the radius of the circle. 13cm
10) AB and CD are two parallel chords of a circle such that
11) AB and CD are two chords of a circle such that AB=6cm, CD=12cm and AB||CD. if the distance between AB and CD is 3cm, find the radius of the circle. 6.7cm
Type -6
1) The length of common chord of two intersecting circles is 30cm. If the diameters of two circles be 50cm and 34cm, calculate the distance between the centres. 28cm
2) Two concentric circles of radii 3cm and 5cm are drawn. A line PQRS intersects one circle at a point P and S and the other at Q and R. If QR= 2cm, determine PQ. (√17-1)cm
3) Two circles of radii 10cm and 8cm intersect and the length of the common chord is 12cm. Find the distance between the centres . 13.29cm
Miscellaneous -1
1) O is the centre of a circle of radius 5cm. P is any point in the circle such that of OP= 3 cm. A is the point travelling along the circumference and x is the distance from A to P. What are the least and the greatest values of x in cm ? What is the position of the points O, P and at these values?
Least value of x is 2cm; when A is on OP produced. Greatest value of x is 8cm.
2) A chord CD of a circle, whose centre O, is bisected at P by a diameter AB .
Given OA= OB=15 cm and OP= 9cm.
a) CD. 24
b) AD. 26.83
c) CB. 13.42
3) The given below shows a circle with centre O in which time diameter AB bisects the chord CD at a point E.
4) Two circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
5) The line joining the midpoints of the two chords of a circle passes through its centre. Prove that the chords are parallel.
6) The figure shows two concentric circles and AD is a chord of larger circle.
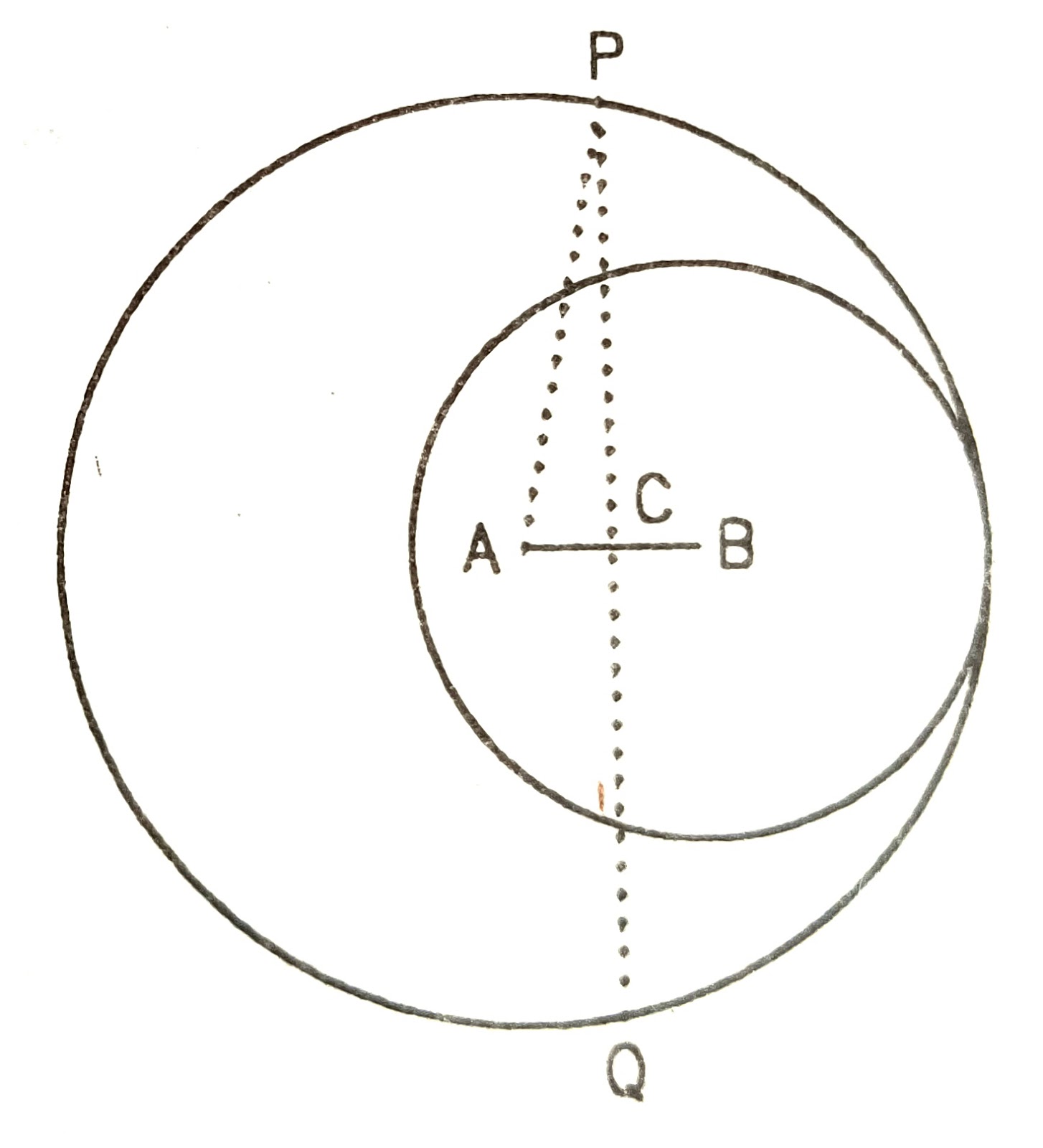
7) Two circles with center A and B and of radii 5cm and 3cm touch each other internally.
8) In figure O is the centre of the circle of radius 5cm. OP perpendiculars to AB, OQ perpendicular to CD, AB||CD, AB= 6cm and CD= 8cm.
9) in figure O is the centre of the circle with radius 5cm OP perpendicular to AB, OQ perpendicular to CD, AB|| CD, AB= 6cm and CD= 8cm.
10) in a circle of radius 5cm, AB and AC are two chords such that AB = AC= 6cm. Find the length of the chord BC. 9.6cm
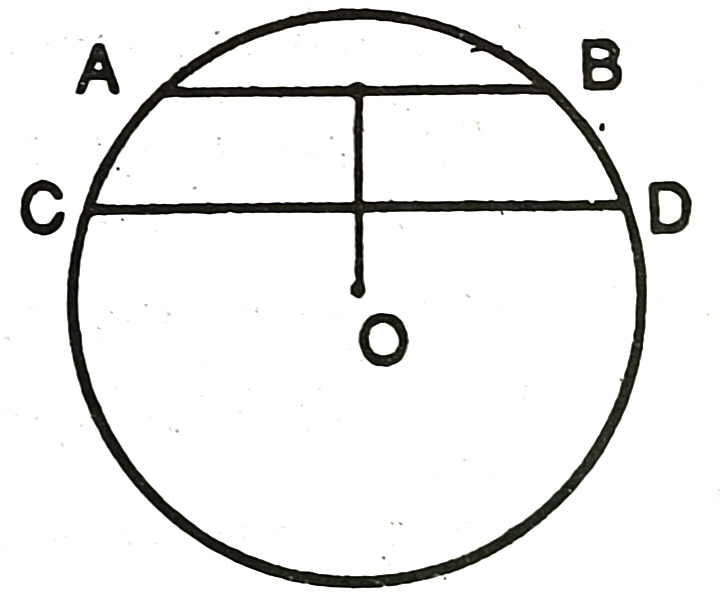
11) Two concentric circles with centre O have A, B, C, D as the points of intersection with the line l as shown in figure. If AD=12cm and BC=8cm, Find the lengths of the AB, CD, AC, BD. 2, 2, 10, 10
12) An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.
13) Chord AB of a circle is tangent to a smaller concentric circle. Given AB=30cm and radius of the smaller circle=8cm. Calculate the length of the radius of the bigger circle.
No comments:
Post a Comment