Point: A point is a mark of position. Thus, a point denotes an exact location.
A fine dot represents a point.
Hence, it has no length, breadth or thickness.
Line segment: The straight path joining two points A and B is called a line segment AB.
A line segment has a definite length.
It has no breadth or thickness.
The distance between the points A and B is called the length of the line segment AB.
Ray: A line segment AB when extended indefinitely in in one direction, as shown is the ray AB. A------------>B
AB has one end point A.
A ray has no definite length.
A ray cannot be drawn, it can simply be represented on the plane on the paper. Thus, to draw a ray would mean to represent it.
Line: A line segment AB when extended indefinitely in both the directions is called LINE AB. It is <-------------->
A line has no end points.
A line has no definite length.
A line cannot be drawn, it can simply be represented on the plane on the paper. Thus, to draw a line would mean to present it.
Sometimes, we label lines by small letters l, m, n, <--->l
Plane: A plane is a surface such that every point of the line joining any two points on it, lies on it.
The surface of a smooth wall; the surface of the top of a table
; the surface of a smooth blackboard, the surface of a sheet of paper, etc., are close examples of a plane.
These surfaces are limited in extent but a geometrical plane extends endlessly in all directions.
Collinear Points: Three or more than 3 points are said to be collinear , if all of them lie on the same line. <---A---B---C-->
In the adjoining figure A, B, C are collinear points, while P, Q, R are non collinear.
Intersecting Lines: Two lines having a common point are called insecting lines.
The point common to two given lines is called their point of intersection.
In the given figure, the line AB and CD intersect at a point O.
Concurrent Lines: Three or more lines intersecting at the same point are said to be concurrent.
In the given figure, the lines l, m, n pass through the same point P. So, these lines are concurrent.
SOME GEOMETRICAL CONCEPT (AXIOM, THEOREM AND COROLLARY)
1) statement : A mathematical sentence which can be JUDGED to be either true or false (but not both), is called a Statement.
Examples:
a) The sum of the angles of a triangle is 180°, is a true statement.
b) The sum of the angles of a quadrilateral is 300°, is a false statement.
c) x + 3 > 8 is a sentence, but not a statement.
2) Proof of a Statement : Providing a geometrical result by using logical reasonings on previously proved and knownt results , is called a proof.
3) Axioms : The basic facts which are taken for granted without proof are called Axioms.
Examples:
a) Halves of equals are equal.
b) The whole is greater than a each of its parts .
c) A line contains infinitely many points.
4) Theorem : A statement that requires a proof is called theorem.
Examples :
a) The sum of all angles of a triangle is 180°.
b) Two parallelogram on the same base and between the same parallel are equal in area.
5) Corollary : A statement whose truth can easily be deduced from a theorem, is called a corollary.
CONCEPT OF ANGLES
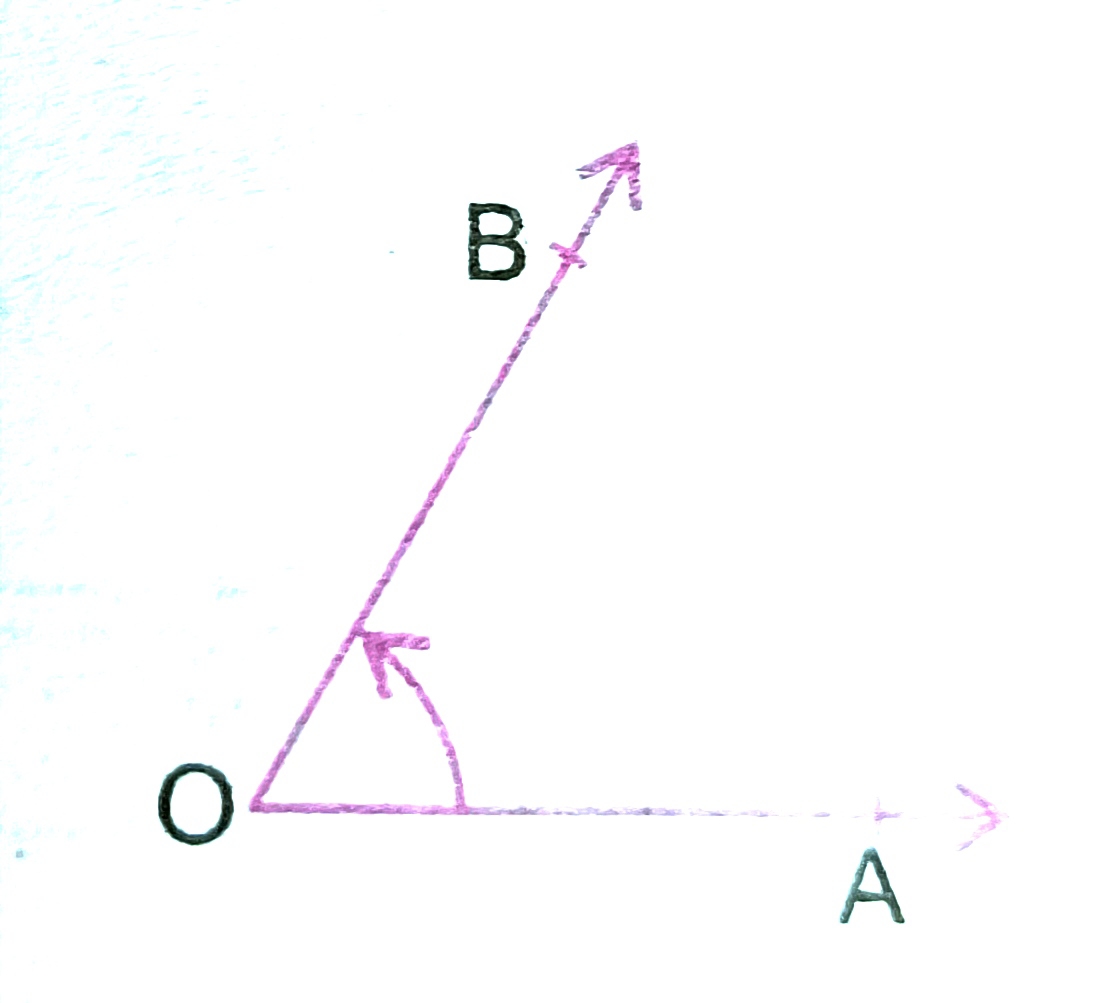
Angle : Two rays OA and OB having a common end point O form angle AOB, written as ang AOB.
And, O is called the vertex of angAOB.
An angle measuring 90° is called a right angle.
Thus, 1 right angle = 90°
1°= 60'
1' = 60"
Kinds of Angle
a) Right angle : An angle whose measure is 90°, is called a right angle.
c) Obtuse-angle: An angle whose measure is more than 90° but less than 180°, is called an obtuse-angle.
e) Reflex-angle : An angle whose measure is more than 180° but less than 360°, is called a reflex angle.
Equal Angles
Two angles are said to be equal, if they have the same measure.
Bisector of an angle
A ray OC is called the bisector of angle AOB, if angAOC = m ang BOC.
In this case, angAOC = ang BOC =1/2 angAOB.
Complementary angles
Two angles are said to be complementary , if the sum of their measure is 90°.
Two complementary angles are said to be complement of each other.
Example : Angles measuring 54° and 36° are complementary angles.
Supplementary Angles
Two angles are said to be supplementary, if the sum of their measure is 180°.
Two supplementary angles are called the supplement of each other.
Example: Angles measuring 130° and 50° are supplementary Angles.
Exercise -1
a) 32° 58
b) 46°31'. 43°30'
c) 34°54'18'. 55°5'52"
d) 2/5 of a right angle. 54
2) Find the supplement of
a) 30°. 150
b) 83°18'24". 96°41'36"
c) 88°46". 91°14'
d) 3/5 of a right angle. 126
3) If (x+9) and (2x -3) are complementary angles, find x. 28
4) If (3x+6) and (2x +14) are supplementary angles, find x. 32
5) Find an angle which equals one-fifth of its supplement. 30
6) Find an angle which equals one-fourth of its complement. 18
7) Find an angle which is 24 more than its complement. 57
8) Find an angle which is 38 less than its supplement. 71
9) Find an angle which is 30° more than one-half of its complement. 50
10) Find an angle which is 24° more than one-third of its supplement. 63
11) Two supplementary angles are in the ratio 5:7. Find the angles. 65/2, 105/2
13) Find two complementary angles are in the ratio 7:3. 126, 54
14) Find the measure of an angle which is 25° more than two-thirds of its complement. 41
15) Find the measure of an angle, if 5 times its complement is 30° less than twice it's supplement. 40
16) Two supplement angles are in the ratio 2:3. Find the angles. 72, 108
Two angle subset to the adjacent angle if they have the same vertex they have a common on they are non common answer in the either side of the common in the given figure a o b b o c are adjacent angles having the same vertex so a common I am OBB and the non common arms on either side of OB we have b+bo3 this is known as addition xcm of adjacent angle linear pair of angles towards in angles acid to be linear pair if the non common answer to opposite ways if the sum of their major is 118 RTO office address coa is a straight line aobboc common linear pair vertically opposite angles to angles are called a tear a vertically opposite angles if the runs from 2 pairs of opposite raise let two lines ABCD interested the point over the vertically opposite
Exercise-2
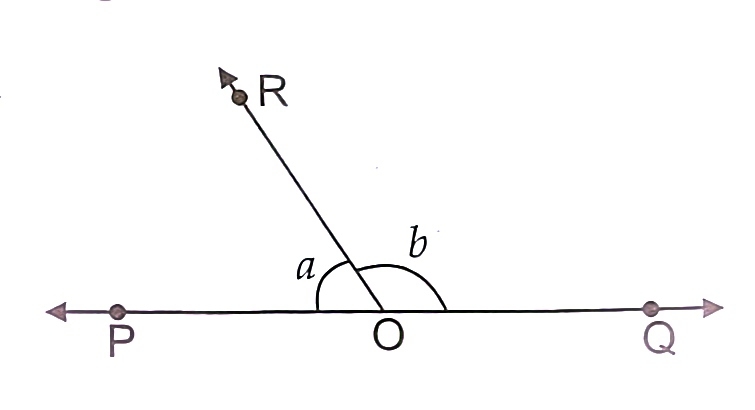
a) if x=72, find the value of y. 108
b) if y= 105, value of x is. 75
2) In the given figure
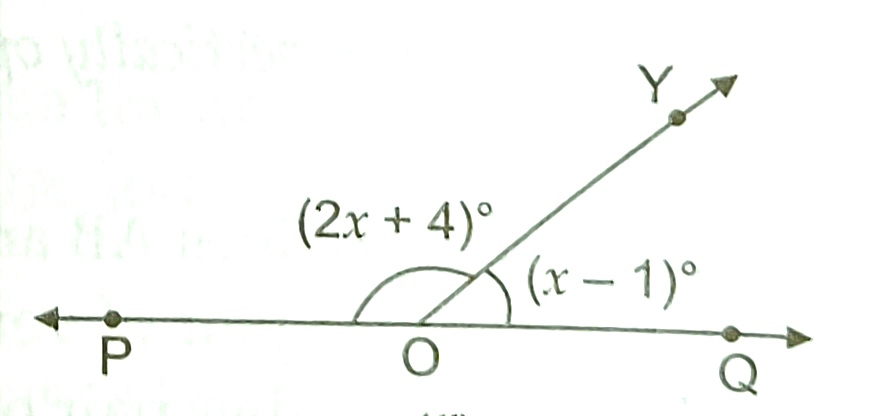
3) In the following figure POQ is a straight line. Find the value of x. 28, 59
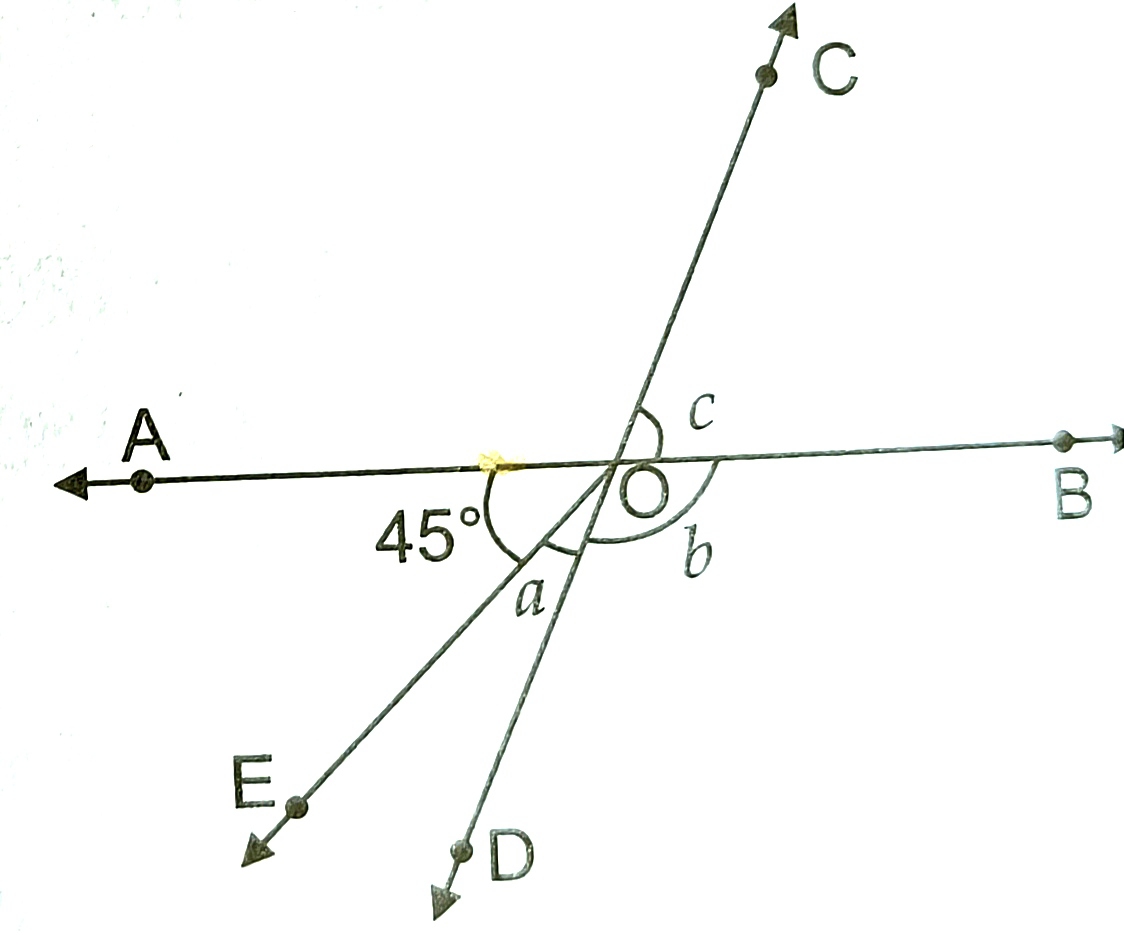
If angAOR=45° and a: b=1:4, find c. 72
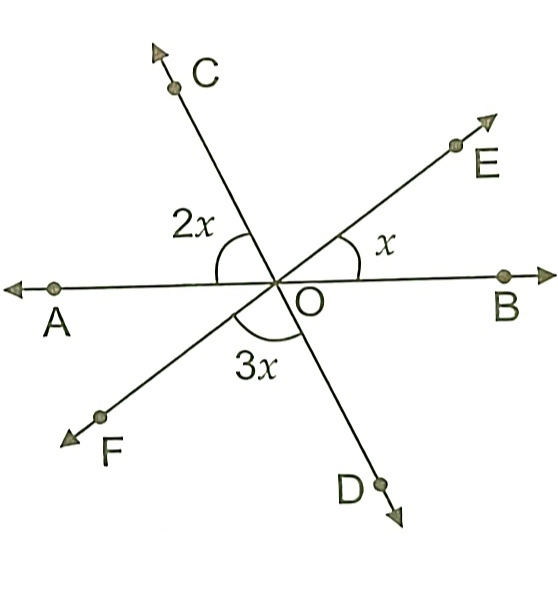
6) In the given figure, l, m and n are three coplanar lines Intersecting at point O.
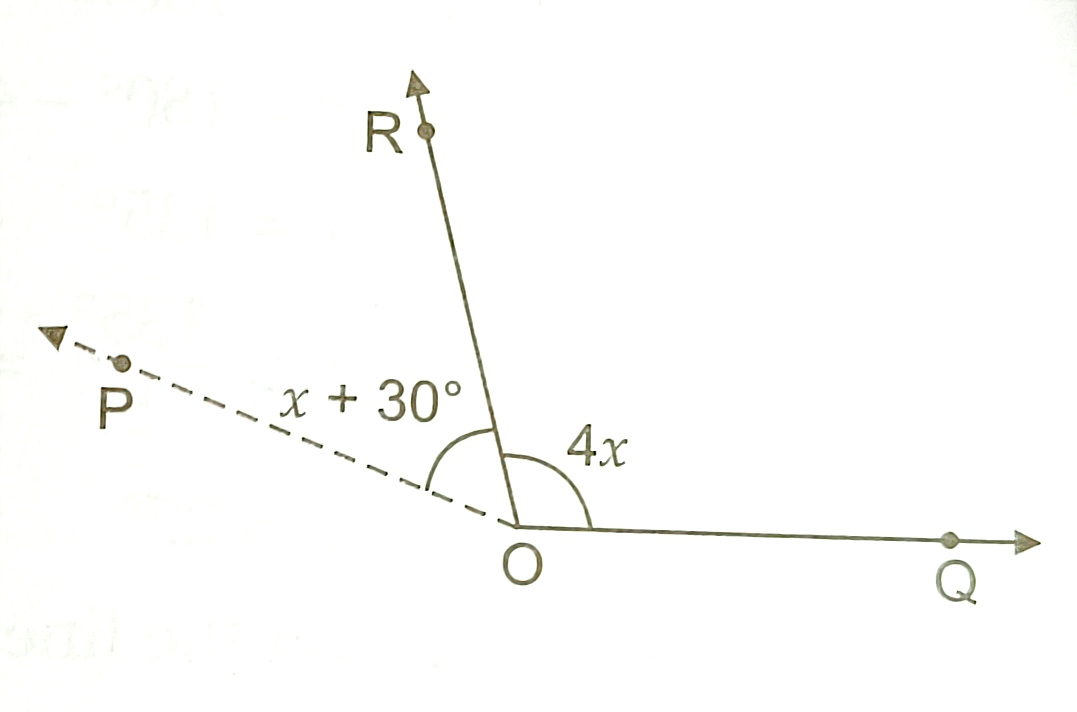
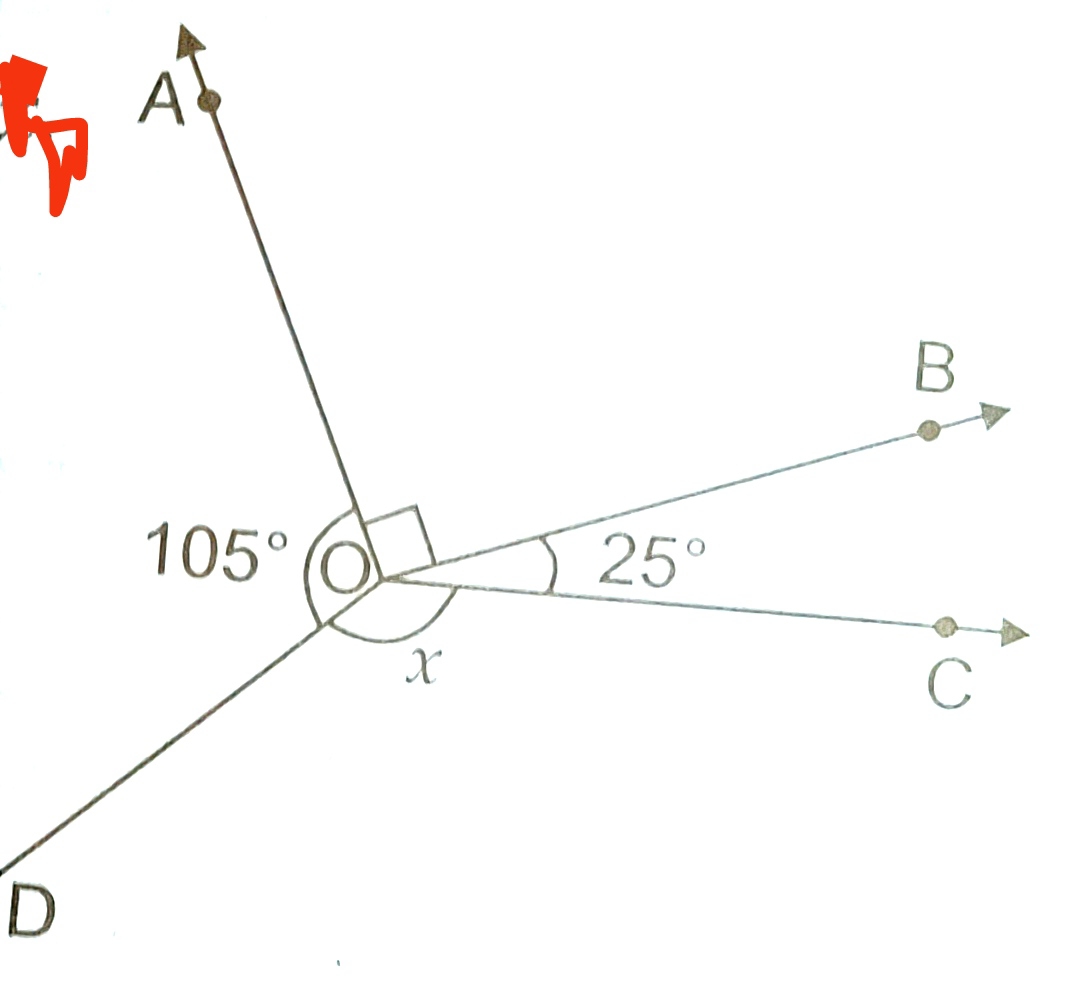
7) In the following figure the value of x. 140
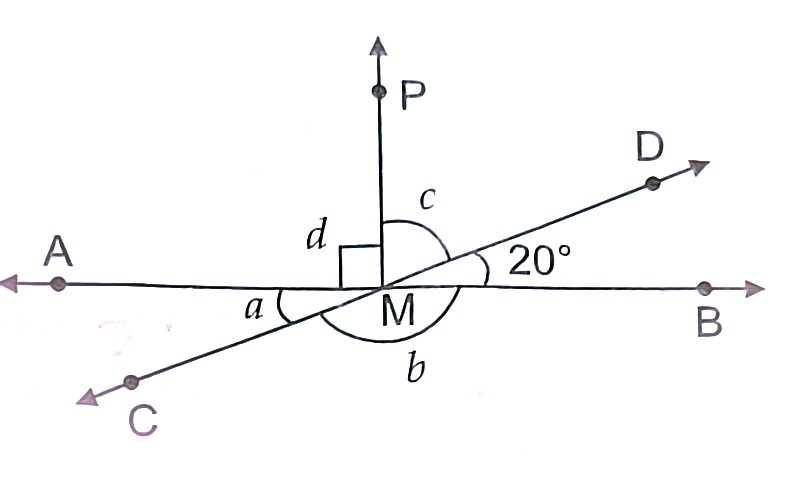
9) In the given figure, lines AB and CD Intersect at M. PM perpendicular AB. If angDMB=20, find the angles a, b, c and d. 20,160,70,90
b) b- a= 50. 65,115
c) 2a= b -30. 50,130
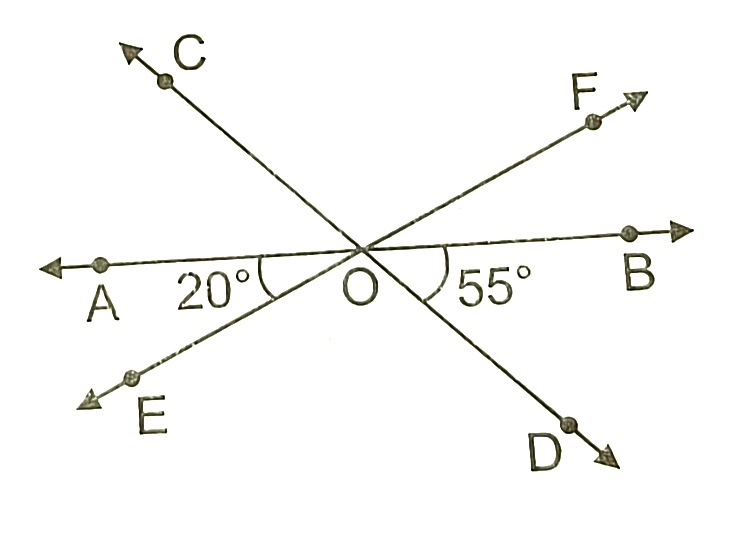
11) In the figure, lines AB, CD, EF intersect at O.
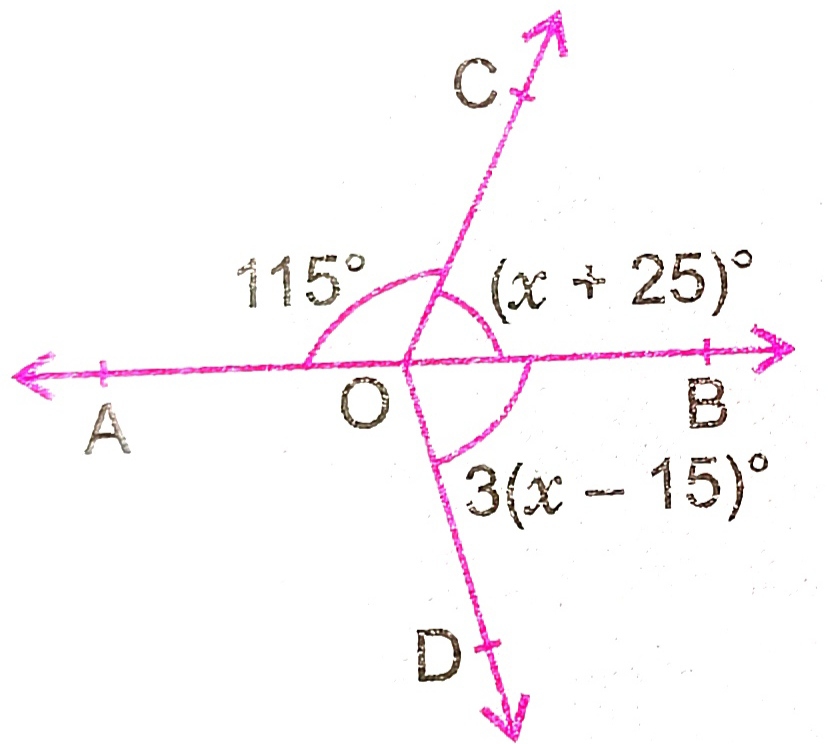
12) In the given figure, AOB is a straight line. If angAOC= 115, angBOC= x+25 and angBOD = 3(x -15), find the value of x.
13) In the given figure, calculate the value of x and hence find the measure of angBOC and angCOD. 15,30,45
14) In the given figure, AOB is a straight line and angCOD=100.
a) The value of x and y, when z=105. 25,30
b) The value of y and z, when x=24. 32, 108
c) The value of x and z, when y=x+2. 26,102
15) In the given figure,
17) Find x. 66.5



















No comments:
Post a Comment