b) Given AD= 1/2 BD, calculate DE, if BC=4.5 cm. 1.5cm
2) In a ∆ PQR, L and M are two points on the base QR such that angLPQ= ang QRP and angRPM= angROP. Prove that
a) ∆PQR and ∆ RPM are similar
b) QL. RM= PL. PM
c) PQ²= QR.QL
3) In the figure, the median BD and CE of ∆ABC meet at G.
a) ∆EGD and ∆ CGB are similar
b) BG= 2GD from (a) above
4) In the figure, P is a point on AB such that AP : PB= 4:3. PQ is parallel to AC.
b) In ∆ARC, ang ARC = 90° and in ∆ PQS, angPSQ=90°. Given QS = 6cm, calculate the length of AR. 3:7
5) In the figure, ABC is a triangle. DE||BC and AD/DB =3/2.
b) Show ∆ADE and ∆ABC are similar. And write down the ratio of DE/BC. 3/5
c) Show ∆DEF and ∆CFB are similar.
6) Calculate the remaining sides of a triangle whose shortest side is 5cm and which is smaller to a triangle with sides 4cm, 7cm and 8cm. 8.75, 10
7) A vertical pole 4m high casts a shadow 1.6m long at the same moment as a flagstaff casts a shadow 12m long. Calculate the height of the flagstaff. 30
8) In a triangle ∆ABC, D and E are points on AB and AC respectively such that DE||BC, prove that ∆ADE and ∆ABC are similar.
If BC =12cm, BD = 7cm, and AD = 8cm,.find the length of DE. 6.4
9) ∆ABC and ∆PQR are similar and ang C=90. If AC= PQ =5cm and QR = 4cm, calculate the length of AB and BC. 17/2, 20/3
9) In a ∆ABC, D is a point on BC such that ang BAD= ang ACB, AB =6cm, AD =5cm and BD = 4cm. If CD = x and AC= y, find x, y. 5,7.5
10) In the adjoining figure find
a) AB b) BC. 2.5, 6
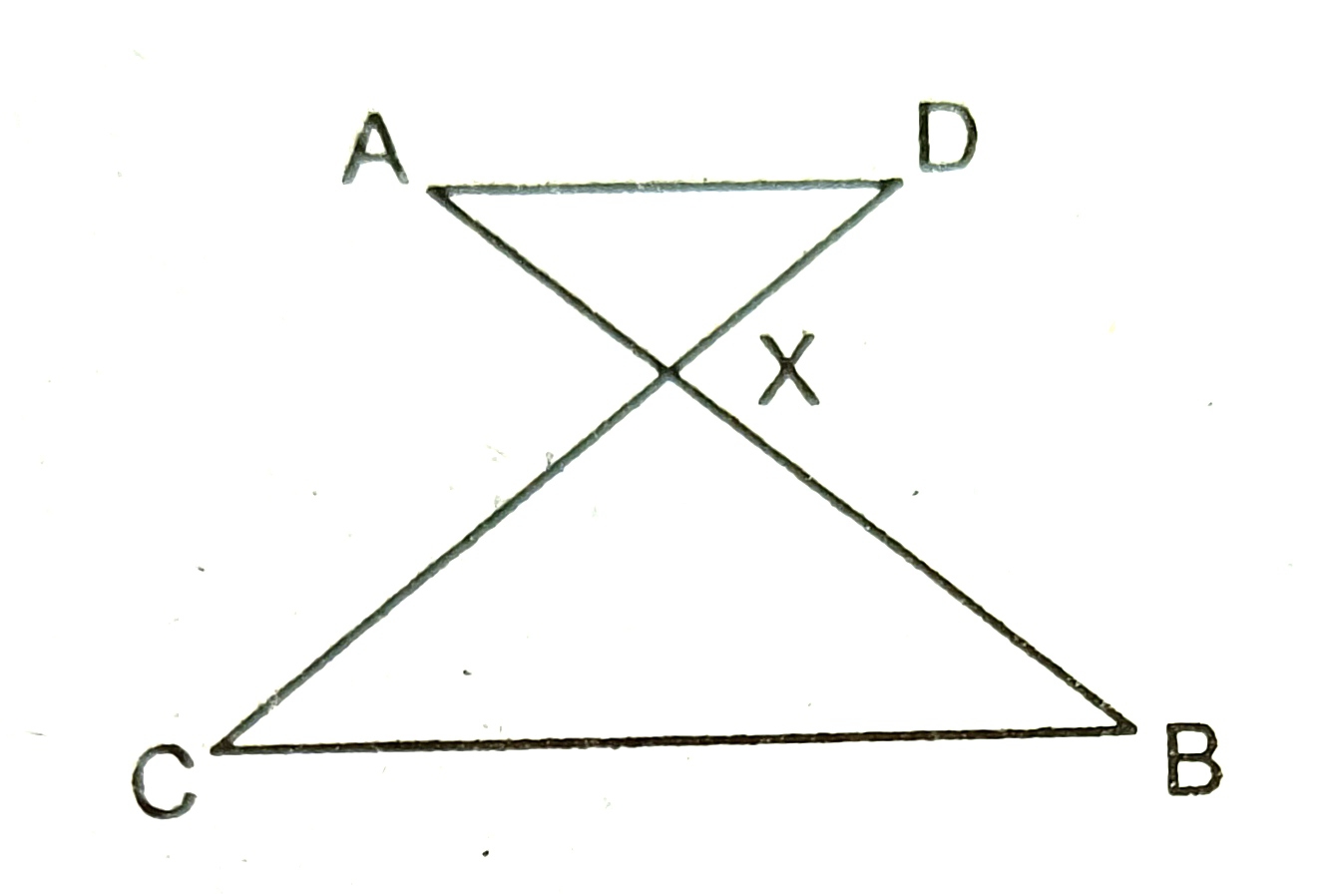
11) In figure, AB and CD Intersect at X. If AX/BX= DX/CX, prove that AD||BC.
12) The perimeter of two similar triangles are 40cm and 25cm. If a side of the first triangle is 15cm, find the length of the corresponding side of the second triangle. 75/8
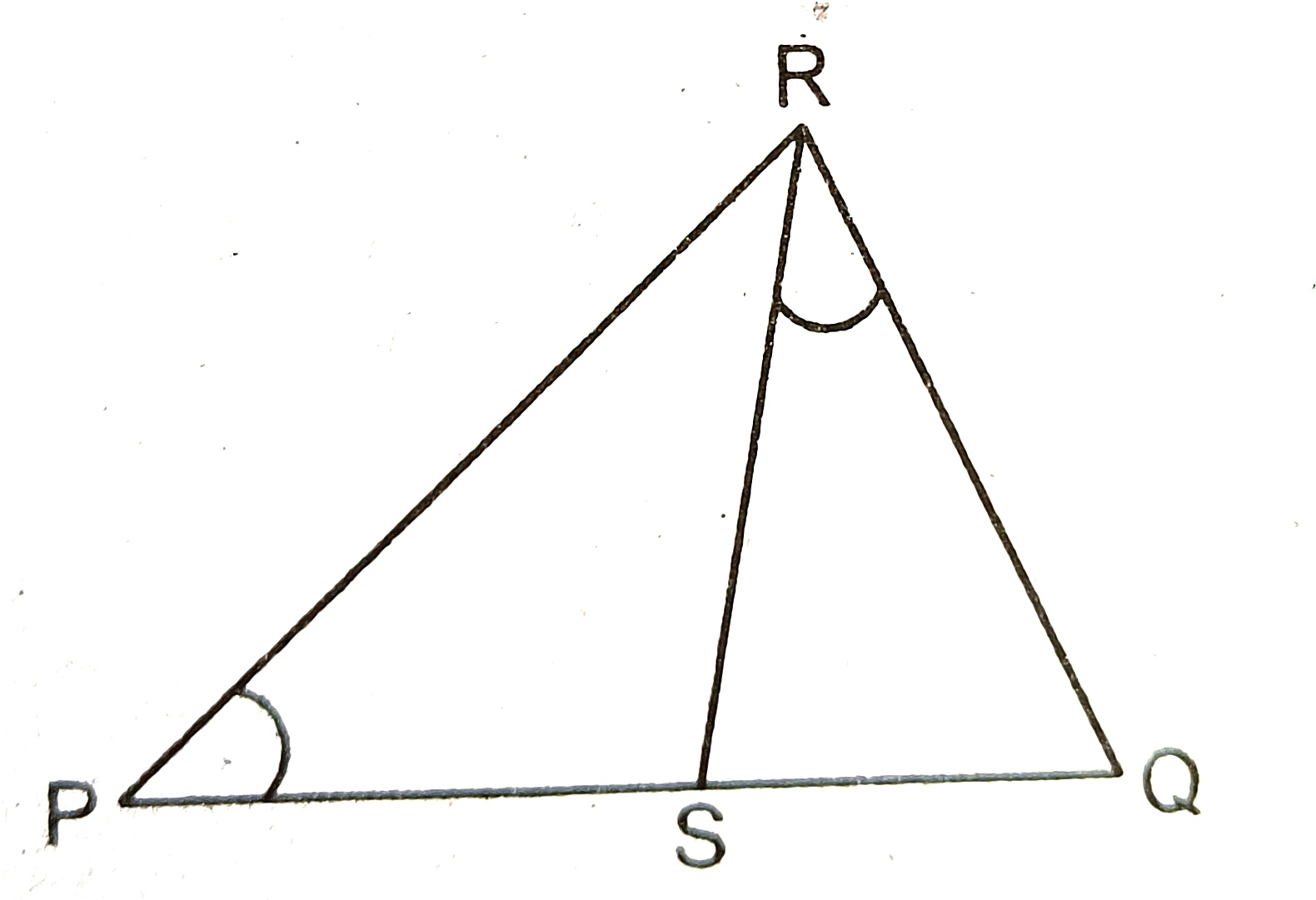
13) In figure, angRPS= angSRQ. show that ∆PQR similar to ∆RQS.
14) Two isosceles triangles have their vertex angle equal. Prove that the triangles are similar.
15) The perimeter of two similar triangles ABC and PQR are respectively 32 and 24cm. If PQ=12cm, find AB. 16
16) D is a point on side BC of a ∆ABC such that angADC and ang BAC are equal. Prove that CA² = DC x CB.
17) In the figure ST||QR, PS=4cm, QS=5cm and PR=8 cm.
a) PT b) TR c) QR/ST. 32/9, 40/9, 9/4
18) In figure DE || BC and BD || FE, AD=5cm, and DB=6cm, AE=3cm
19) If one diagonal of a trapezium divides the other diagonal in the ratio 1:2 prove that one of the parallel sides will be half the other.
20) PQRS is a parallelogram, M is the midpoint of PS. RM intersect SQ in X. RM produced meets QP produced Y prove XY = 2RX
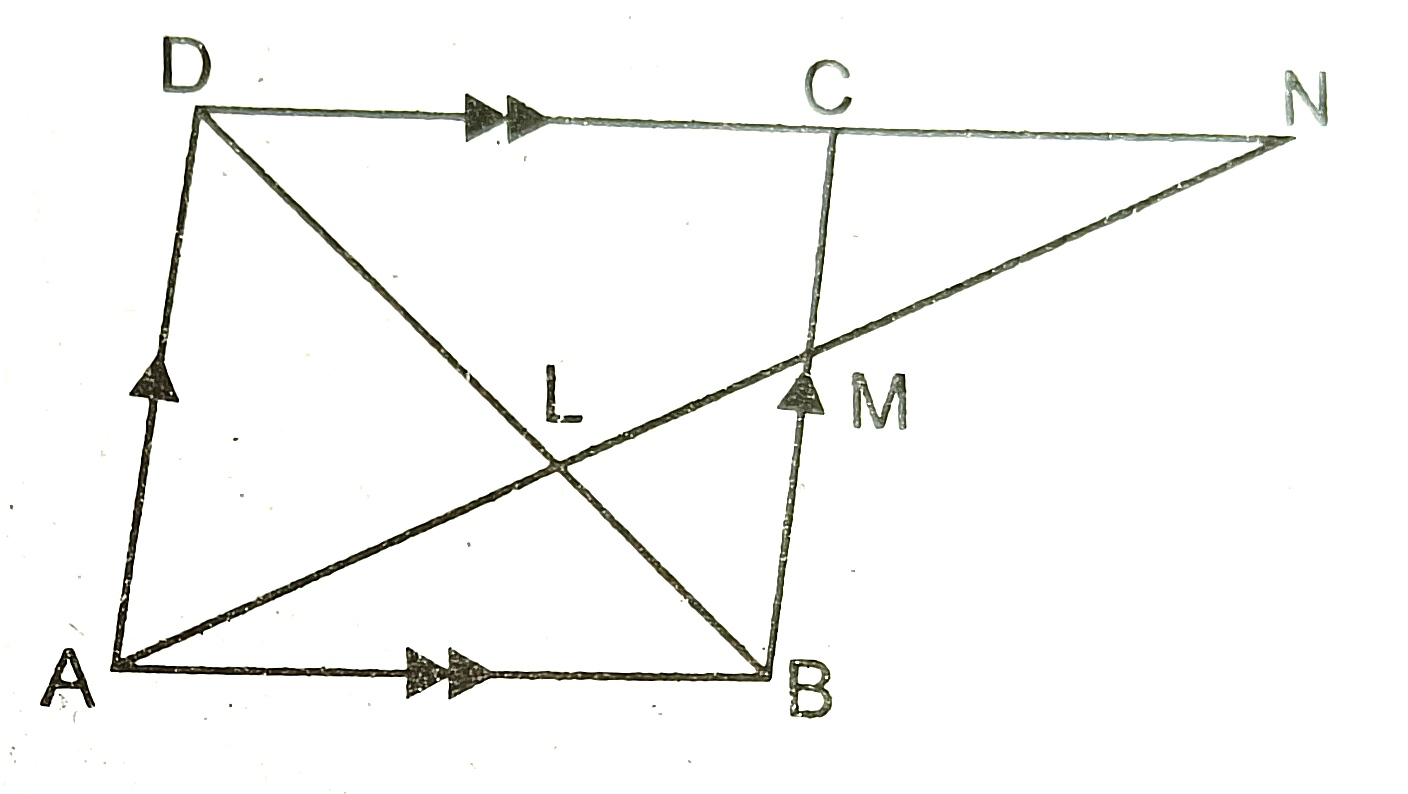
21) ABCD is a parallelogram. A straight line is drawn through A meeting lines BD at L and BC at M and DC produced at N. Prove that AL/LN= AM/AN.
22) ABCD is a parallelogram. E is any point on BC . AE and BD intersect at O. Prove that AO x OB = OD x OE.
23) ABCD is a trapezium in which AD|| BC. AC and BD Intersect at E. If ∆ AED similar to ∆BEC, show that AB = DC.
24) PQR is an equilateral triangle. The base QR is produced both ways to X and Y such that QR = QX = RY. If PX and PY are joined , show that the triangles PQX and XPY are equiangular and hence, show PX² = 3QR².
25) AF is the median of ∆ABCb. FD and FE are bisectors of angAFB and angAFC meeting AB and AC at D and E respectively. Show that DE||BC.
b) DN²= DM x AN.
27) In the adjoining figure, LM is parallel to BC. AB = 6cm, AL =2cm and AC =9cm.
28) In figure, ABCD is a trapezium with AB|| DC and AB = 1/2 DC. Prove that O is the point of trisection of diagonals AC and BD.
29) In the figure alongside, PQRS is a parallelogram. PQ =16cm, QR = 10cm. L is a point on PR such that RL : LP = 2:3. QL produced meets RS at M. And PS produced at N .
b) Name a triangle similar to Triangle RLM. Evaluate RM as a fraction. 32/3
No comments:
Post a Comment