CIRCLE (A- Z)C++

EXERCISE -1

1) Find the area a circle of radius 

a) 7cm                                  154cm²

b) 7.7cm.                     186.34 cm²        

2) A horse is tied to a pole with a 28m long string. Find the area where the horse can graze. 2464m²

3) A rope by which a cow is tethered is increased from 12m to 23m. How much additional ground has it to brouse over. 1210m²

4) Find the circumference and area of a circle of :

a) radius 14 cm.         88cm, 616cm²

b) radius 2.1 m.         13.2m, 13.86m²

c) diameter 35 cm.       110cm, 962.5cm²

d) diameter 77 cm.      242cm, 4658.5 cm²

e) radius 21 cm.         132cm, 1386cm²

f) diameter 14cm.        44, 154cm²

g) 4.2cm.                       26.4cm

h) 7.2cm.                      45.26

EXERCISE - B

1) Find the diameter of a circle and its circumference if its area is:

a) 6.16 m².          2.8m,  8.8m

b) 394.24cm².     22.4cm, 70.4cm

c) 25π cm.          10cm, 10π cm

d) 77/8 m².                  3.5m

e) 15400cm².             70cm, 440cm

f) 6.16cm².                 8.8cm

2) Find the radius of a circle and area if its circumference is:

a) 176cm. 28cm, 2464cm²

b) 11 meter. 1.75m, 9.625m²

c) 16πcm. 8cm, 64π cm²

d) Find the radius of a circle whose circumference is 66cm. 10.5 cm

e) if the circumference of a circle is 132 cm, find its radius and area. 21,1386

EXERCISE - C

1) The diameter of a wheel is 1.26m. How far will it travel in 500 revolutions.  1980m

2) The diameter of the driving wheel of a bus is 140cm. How many revolutions per minute must the wheel make in order to keep a speed of 66km per hour?     250

3) How many times will a wheel of diameter 105cm rotate in covering a distance of 330m.       100

4) if the wheel of a bicycle has a diameter of 84cm, find

a) the distance travelled by the cyclist after one rotation of the wheel.     264cm

b) the number of rotations of the wheel if the cyclist covers a distance of 1.65 km. 625

5) A bicycle wheel is 1 m 26cm in diameter. Calculate 

a) the distance travelled in one rotation of the wheel.      96cm

b) the number of rotations of the wheel needed to cover 1.98 km.    500

6) A wheel of cart is making 4 revolution per second. if the diameter of the wheel be 84cm, find the speed.    38.016 km/hr

7) How many times will the wheel of a car rotate in a journey of 88 km if it is known that is known known that the diameter of the wheel is 56cm?  50000

8) A bicycle, wheel makes 5000 revolutions in a moving 11km. Find the diameter of the wheel.     70cm

EXERCISE - D

1) Find the radius of a circle whose area is equal to the sum of the areas of three circles whose radii are 3cm, 4cm, and 12cm.        13cm

2) The circumference of a circle exceeds the diameter by 16.8cm. Find the radius of the circle.       3.9

3) The perimeter (circumference) of two circles are in the ratio 2:3. Find the ratio of their areas. 4:9

4) The minute hand of a clock is √21 cm long. Find the area described by the minute hand on the face of clock between 7.00a.m and 7.05a.m. 5.5 cm²

5) The short and long hands of a clock are 4cm and 6cm long respectively. Find the sum of the distance, travelled by their tips in 2 days. 1911cm

6) The minute hand of a clock is 10cm long. Find the area on the face of the clock described by the minute hand between 9am. And 9:35am. 183.33cm²

7) An archery target has three concentric regions I, II, III. The diameter of the circles are in the ratio 2:3:4. Find the ratio of their areas. If the area of the smallest region is 20cm², find the area of the region II and III. 4:9:16, 25,35cm² 

8) A field is in the form of a circle. A fence is to be erected around the field. The cost of fencing would be ₹2640 at the rate of ₹12 per metre. then the field is to be thoroughly ploughed at the cost of ₹0.50 per m². What is the amount required to plough the field? ₹1925

EXERCISE - E

1) A copper wire, when bent in the form of a square encloses on area of 121 cm². If the same wire is bent into the form of a circle, find the area of the circle.         154cm²

2)  In an equilateral triangle of side 24cm, a circle is inscribed touching its sides. Find the area of the remaining portion of the triangle.√3=1.732). 98.55cm²

3) A copper wire, when bent in the form of a square encloses an area of 484cm². If the same wire is bent in the form of a circle,. Find the area enclosed by it. (π=22/7). 616cm²

4) A wire is in the shape of a circle of area 3850 cm². If the same wire is bent in the form of a square, find the area of the square. 3025cm²

5) A metal wire is bent in the shape of a square of area 484cm². If the same wire is bent to form a circle, find the area enclosed. 616cm²

6) What is the area of the circle the circumference of which is equal to the perimeter of a square of side 11cm. 154cm²

7) A wire is bent in the form of a square of area 1936 cm². If the same wire is bent to form a circle, find the radius of the circle and area enclosed. 28cm, 2464cm²

8) A wire is in a circular shape of area 5544 cm². If the same wire is bent in the shape of a square, find the length of a side of the square and its area. 66cm, 4356 cm²

9) A 72cm long piece of wire is bent into the form of a semi circular are bounded by its diameter. Find the radius. 14cm

10) A wire is looped in the form of a circle of radius 28cm. It is rebent into a suare form. Determine the length of the side of the square. 44cm

EXERCISE - F

1) Find the area of a circular ring whose external and internal diameters are 20cm and 6cm respectively?                         286 cm²

2) A road which is 7m wide surrounds a circular park whose circumference is 352m. Find the area of the road ?             2618 m² 

3) The radius of the circular Garden is 100m. There is a track 10m wide around it. Find the area of the track . 6600m²

4) The inner circumference of a circular track is 440m. The track is 14m wide. Find the diameter of the outer circle of track. 168m

5) A race track is in the form of a ring whose inner circumference is 440m and Outer circumference is 506m. Find the width of the track and also the area. 10.5m, 4966.5m²

6) The inner circumference of a circular track is 220m. The track is 7cm wide everywhere. Calculate the cost of putting up a fence along along the outer circle at ₹2 per minute. ₹528

7) The circumference of a circular plot is 220m and a 14m wide concrete track runs around outside the plot. Find the area of the track. 3696m²

8) A race track is in the form of a ring whose outer circumference is 440m and the width of the track is 7m. Find the area of the track. 2926m²

9) The outer circumference of a Circular racing track is 220m. The track is everywhere 7m wide. Calculate the cost of levelling the track at the rate of 50 paise per m². (π=22/7). ₹693

10) A circular park of diameter 30 m is surrounded by a circular path of uniform width 5 m. Find the area of the path. 550m²

11) The area of the ring between two concentric circles is 990 cm². Find the radii of the two circles if their sum is 35cm. 22cm, 13cm

12) A circular pond of diameter 28 m is surrounded by a path 7m wide . Find the area of the path. 770m²

13) Find the area of a 2m wide circular path surrounding a circular plot of radius 20m. 264m²

14) The area of the ring between two concentric circles is 3168 cm². Find the radius of the two circles if

a) their sum is 42cm. 33cm

b) their difference between is 28 cm. 9cm 

15) Two circles touch externally. The sum of their areas is 130π sq.cm and the distance between their centres is 14cm. Find the radius of the circle. 11cm, 3cm

EXERCISE - G

1) The area of a circle inscribed in an equilateral triangle is 154cm². Find the perimeter of the triangle. Give your answer Correct to one decimal places. (π=22/7, √3=1.73). 72.70 cm 

2) A paper is in the form of a rectangle ABCD where AB= 22cm and BC =14cm. A semicircular portion with BC as diameter is cut off off. Find the area of the remaining paper. 231cm²

3) A rectangular field is 50m long and 32m wide. A well is dug in one of its corner. If the radius of a well is 3.5m. Find the area of the remaining field. 1561.5m²

4) A park is in the form of a square, one of whose sides is 50m. At the centre of the park is a circular lawn. If the area of the park excluding the lawn is 2346m², find the cost of fencing the lawn at the rate of ₹1.50per m. ₹66

5) A student takes a rectangular piece of paper 30cm long and 21cm wide. Find the area of the greatest circle he can form, from the paper. Also find the area of the paper left after cutting out the circle. 346.5 cm², 283.5 cm².

6) A cube whose edge is 20cm long has a circle 20cm diameter on each of its faces painted black. What is the total area of the unpainted of the cube? 3600/2 cm²

EXERCISE - H

1) A semicircular grassy plot is attached to a rectangular plot 40m by 28m along its width. Find the cost of fencing the (combined) plot at ₹1.25 per meter. ₹190

2) If the diameter of a semicircular protractor is 14cm, then find its perimeter. 36m

3) A 54 cm long piece of wire is bent into the shape of a semi-circular are bounded by its diameter. Find its radius. 10.5cm

EXERCISE -I

1) A chord AB of a circle of radius 15cm makes an angle of 60° at the centre of the circle. Find the area of the major and the minor segments. (Take π=3.14, √3= 1.73). 20.4cm², 686.222cm²

2) AB is a chord of circle of radius 10cm. The chord subtends a right angle at the centre. Find the area of the minor segment. (Use π=3.14). 28.5cm²

3) Find the area of a sector of a circle of 7cm diameter whose Central angle is 100°. 10.66cm²

4) Find the area of the sector of a circle of a Circle whose Central angle is 30° and the radius of the circle is 42cm. 462cm²

5) A sector is cut off from a circle of radius 21cm. The angle of the sector is 120°. Find the length of the ARC and the area. 44cm, 462 cm² 

6) The perimeter of a certain sector of a circle of radius of 5.6m is 27.2m. Find the area of the sector. 44.8cm²

7) The perimeter of a sector of a circle of radius 5.2cm is 16.4cm. Find the area of the sector. 15.6cm²

8) A sector is cut from a circle of radius 21cm. The angle of the sector is 150°. Find the length of its arc and area. 577.5 cm²

9) A chord AB of a circle of radius 10cm makes a right angle at the centre of the circle. Find the area of the major and minor segments. (π=3.14). 28.5cm²

MISCELLANEOUS - 1

1) A sheet of paper is in the form of a rectangle ABCD in which AB=40cm and AD=28cm. A semicircle portion with BC as diameter is cut off. Find the area of the remaining paper. 812cm²

2) A circular disc of 6cm radius is divided into three sectors with Central angles 120°, 150°and 90°. What part of the whole circle is the sector with Central angle 120°? Also, give the ratio of the areas of the three sectors. 1/3 (area of the circle)

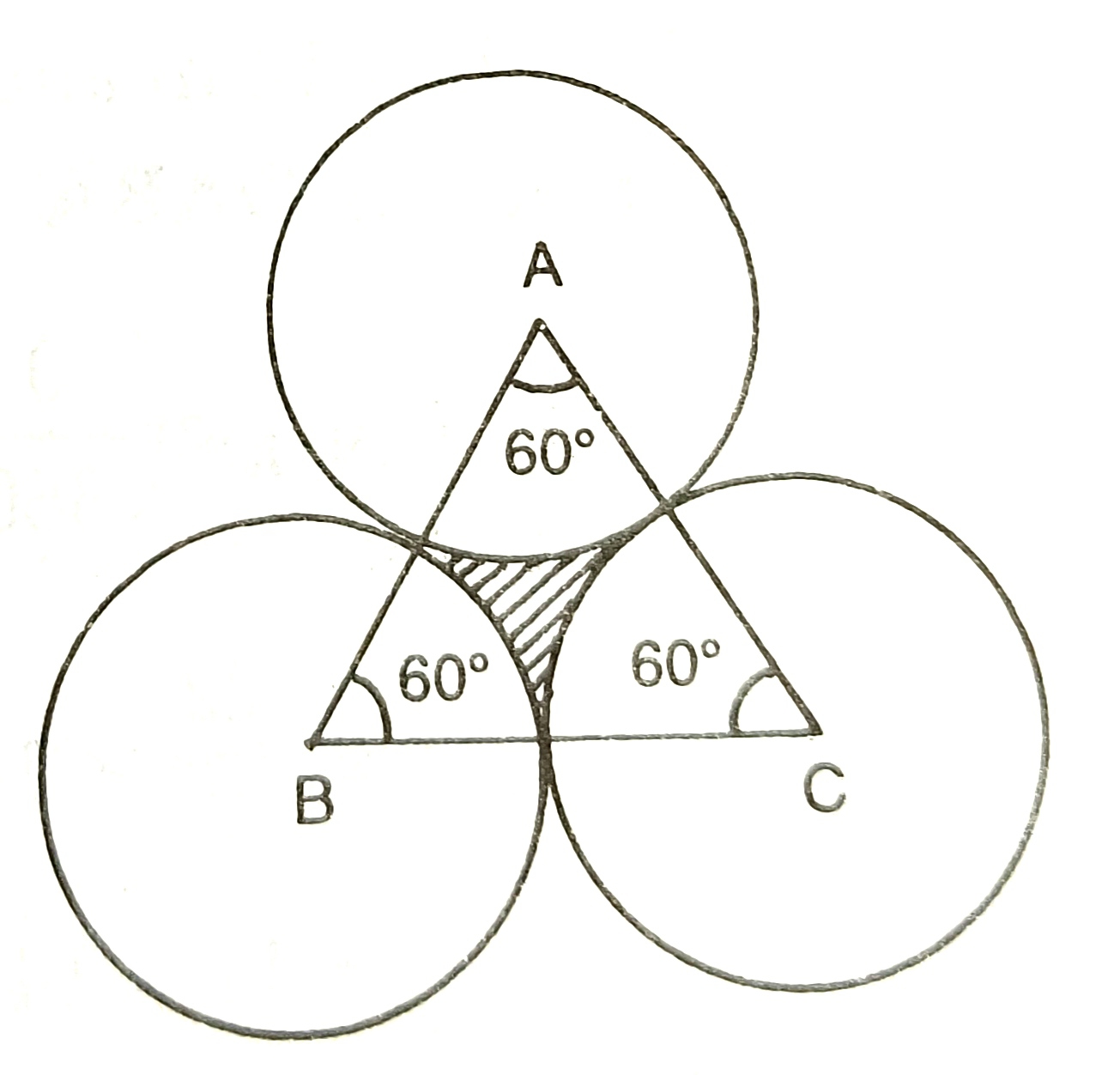
3) There is an equilateral triangle of which the side is 1cm. with all the three corners as centres, circles are described each of radius 1m.   

a) calculate the area common to all the circles circles and the triangles. 1.571m²

b) The area of the remaining portions of the triangle. 0.161m²

4) The area of an equilateral triangle is 17320.5cm². About each angular point as center, a circle is described with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. 1620.5cm²

5) A horse, left for grazing inside a rectangular enclosure 40mx36m, is tethered to one corner of the field by a rope 14m long. Find the area of the quadrant over which the horse can graze. 154m²

6) How many plants can be planted in a circular garden of circumference 26.40 km if a space of 600 cm² is to be allowed for each plant ? 924

7) A circle of circumference 88cm is cut out of a square sheet of paper of side 30 cm. What is the area of the paper left ? 284cm²

DIAGRAMMATIC QUESTIONS 

1) A garden is made up of a rectangular patch of grass and two semi-circular ponds, as shown in the figure. If the length and width of the rectangular patch are 24 m and 14 m respectively,

 Calculate 

a) the perimeter of the garden.       92m

b) the total area of the garden.        490m²

2)  A rectangle of length 35 cm and width 28cm has a semicircle cut out from each of its two sides, as shown. 

Find the area of the shaded portion.      364cm²

3) If ABCD is a rectangle, 

find the area of the shaded portion.      45.84 m²

4) Two semi-circle of equal radii are cut out of a semi-circular piece of cardboard. 

Find the area of the shared portion.         38.5 m²

5) A rectangle encloses four circles. The radius of each circle is 7cm. 

Calculate the area of

a) rectangle.         784 cm²

b) the shaded portion.           168 cm²

6) Find area of the shaded portion formed by a semi-circle placed above the square.   

                                                 68.25 cm²

7) PQRS is a diameter circular radius 6cm. The lengths PQ, QR, and RS are equal, Semicirles are drawn on PQ and QS as diameters as shown in the figure. Find the perimeter of the shaded region.    28.3cm

8) The outer circumference of a circular racing track is 220m. The track is everywhere 7m wide. Calculate the cost of levelling the track at the rate of 50 paise per minute.                          ₹693

9) The minute hand of a clock is 10 cm long. Find the area on the face of the clock described by the minute hand between 9 a.m. and 9:35 a.m.   183.33

10) A chord AB of a circle of radius 10 cm makes a right angle at the centre of the circle. Find the area of the major and minor segments.       285.5, 28.5

11) For equal circles, each of radius 5 cm, touch each other as shown in the figure. Find the area between the circles.   21.5

12) The area of an equilateral triangle is 17320.5cm². About each angular point as centre, a circle is described with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles.   1620.5 cm²

13) A horse, left for grazing inside a rectangular enclosure 40 x36 m, is tethered to one corner of the field by a rope 14m long. Find the area of the quadrant over which the horse can graze.           154 m²

14) Calculate the area of the shaded sector region shown in the figure. π= 22/7).                         17.3 cm²

15) It is proposed to add to a square lawn measuring 58m on a side, two circular ends , the centre of each circle being the point of intersection of the diagonals of the square. Find the area of the whole lawn.          4325.14 cm²

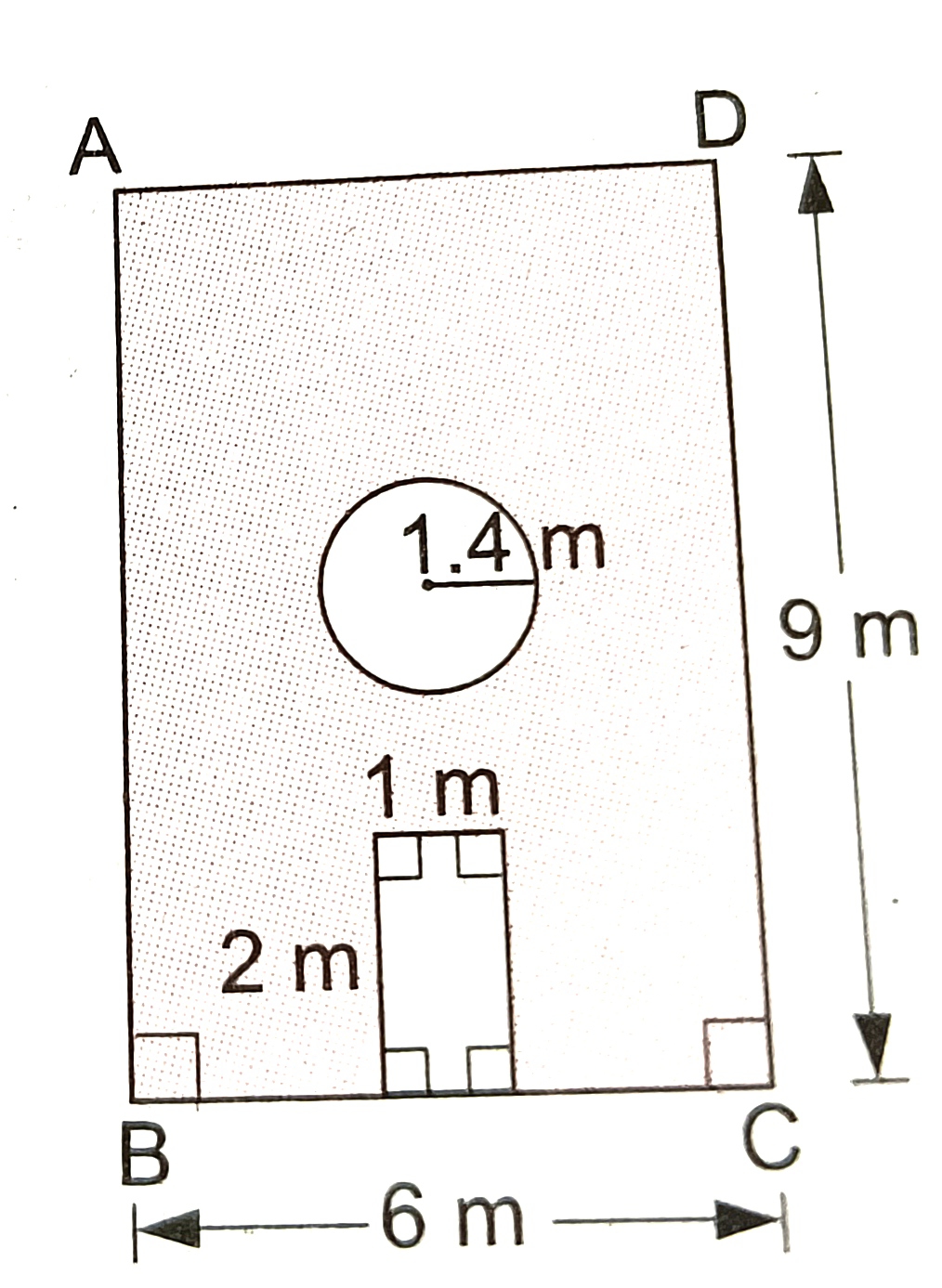
16) The perimeter of the adjoining figure, a semi-circle described on AB as diameter is 7.2cm. Find r the radius of the semi-circle. (π=22/7)

17) In the adjoining figure, the area enclosed between the concentric circles is 770 cm². Given that the radius of the outer circle is 21cm, calculate the radius of the inner circle.  

18) In the adjoining figure ABCD is a square inscribed in a circle of radius 7cm. Calculate

a) the area of the circle.

b) the area of the shaded portion. (π=22/7)

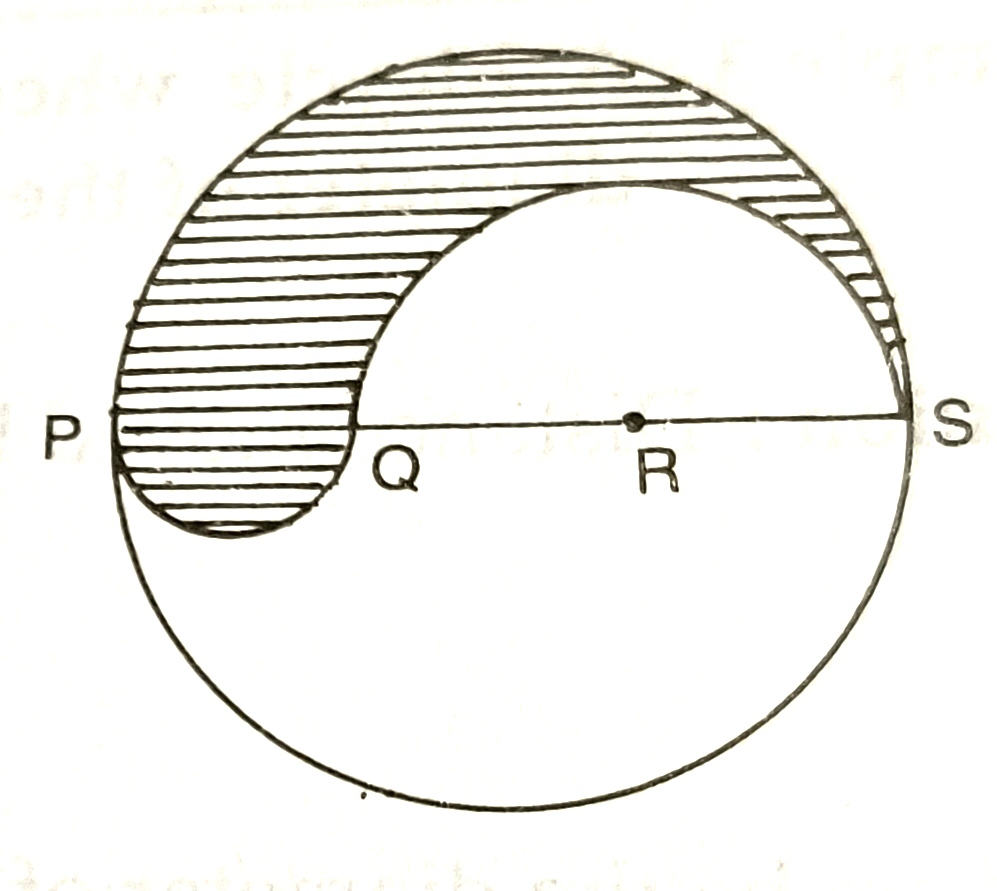
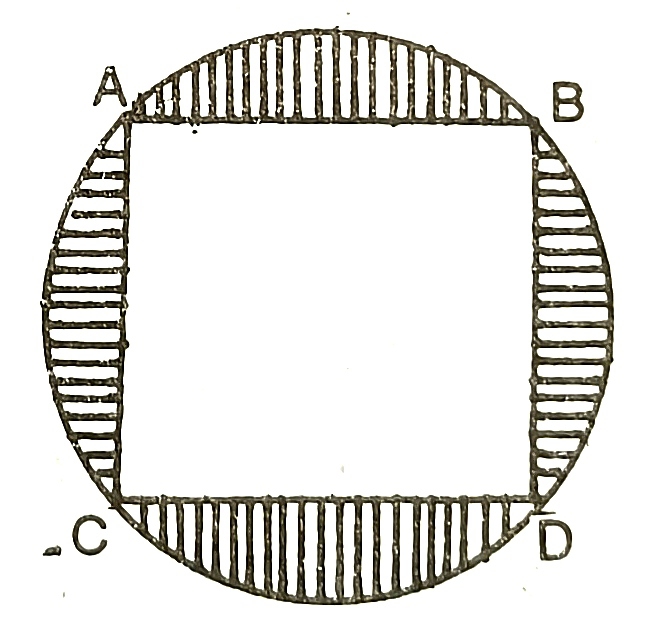
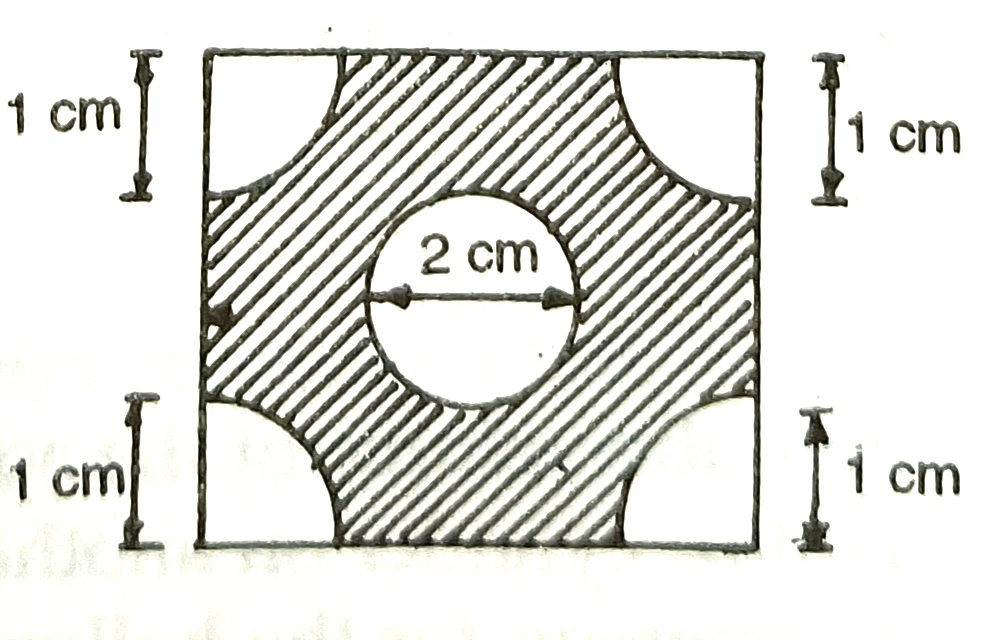
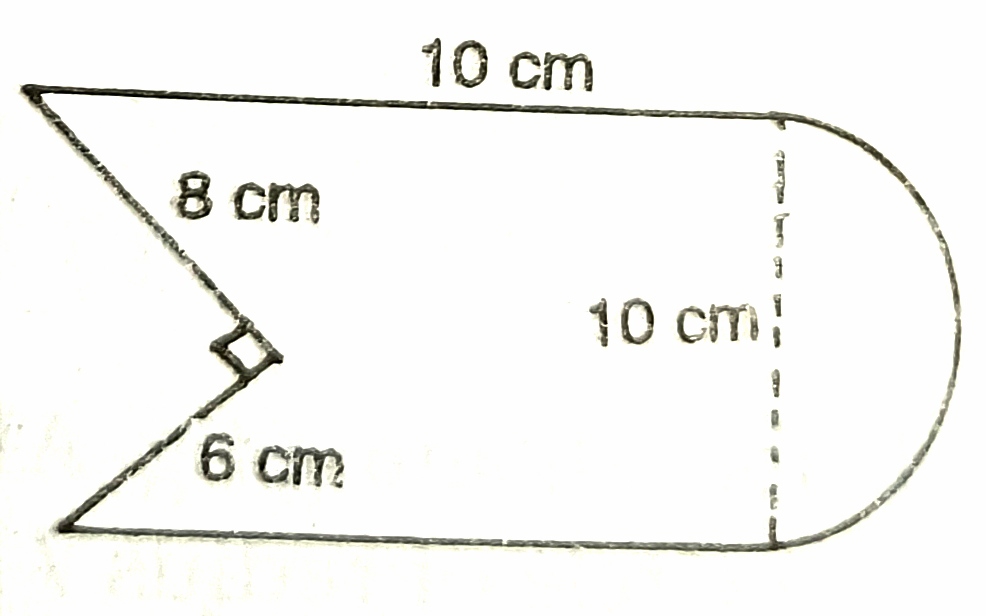
19) ABCD is a square of side 4cm. Find the area of the shaded portion. Use π=3.14 and give your answer correct to one place of decimal.

20) The diameter represents the wiper of a car. With the dimensions given in the diagram, calculate the shaded area swept by the wiper. (π=22/7)

21) Find the area of the adjoining figure in sq cm. Correct to one place of decimal. (π=22/7).

22) Find the perimeter and area of the shaded portion of the adjoining figure, give your answer correct to 3 significant figures. (π=3.14)

23) The adjoining figure consists of a rectangle and a semi-circle. Find its area and perimeter.          532,88

24) The adjoining figure shows the inner boundary of a 600m running track which has two parallel straight lines each of length 200m and two Semicircular ends.

(Assuming π=3.142, calculate the radius of each semi-circular end correct to the nearest 1/100 m).       31.83

25) Four cows are tethered at four corners of a square plot of side 50m, so that just cannot reach one another. What area will be left ungrazed.          535.7m²

26) From the given figure, calculate the area of the shaded portion.       30.57cm²

27) The diagram shows the inner boundary of a 400m running track which has two parallel straights-- each of length 100m and two Semicircular ends. Assuming π=3.142.       31.88m, 9548m²

28) ABCD represents a flower bed. If OA= 21m and OC= 14m, find area of the bed.                       192.5m²

29) A wire when bent in the form of an equilateral triangle encloses an area of 121√3 cm². If the same wire is bent into the form of a circle, find area of the circle.                      346.5cm²

30) In the given figure, diameter of the biggest semi-circle is 108 cm, and diameter of the smallest circle is 36cm. Calculate area of the shaded portion.   1272.9 

31) In the given figure, the square ABCD is divided into five equal parts all of the same area. The central part is circular and the lines AE, BF, HD lie along the diagonals AC and BD of the square. If AB= 11cm, calculate

a) the radius and circumstance of the central part.     2.78,17.47, 25.37

b) the perimeter of the part ABFE.  

32) The boundary of the shaded portion in the given figure consists of three Semicircular areas, the smaller ones being equal. If the diameter of the larger one is 14cm, calculate:

a) the length of the boundary.        44cm

b) the area of the shaded part.     77cm²